Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 20
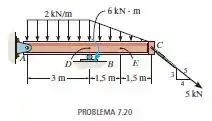
Determine as forças normal e cortante e o momento fletor nos pontos e da viga com o trecho em balanço. O ponto está localizado logo à esquerda do suporte de rolete em , onde o momento de binário atua.
Passo 1
Fala aíiiii... belezinha?
Nessa questão vamos precisar dos conceitos de estática pra somatório de forças e momento:
- Em :
- Em :
- E momento:
E já vamos mandar o diagrama de corpo livre maroto:
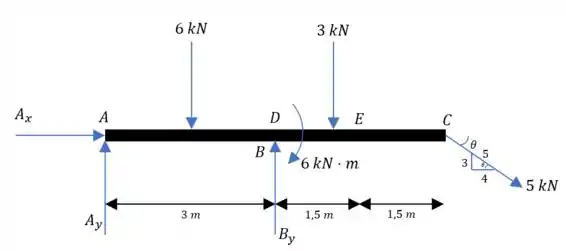
Lembrando que a gente pode substituir a carga distribuída por uma equivalente pontual. Nesse caso vamos até dividir a carga em duas partes:
- a retangular, que fica localizada bem na metade:
- a triangular, que NÃO fica na metade, heim... fica a 1/3 da distância da “base “do triângulo:
Passo 2
Vamos achar esse monte de reação de apoio, então...
Fazendo o somatório das forças em :
Em :
Para o momento:
Daí:
Passo 3
Fazendo o corte em , para ficar com o segmento :
Fazendo o somatório de forças em :
Em :
E para o momento:
Passo 4
E agora fazendo o corte em :
Lembrando que agora precisamos calcular, de novo, qual é a carga equivalente dessa carga distribuída porque pegamos só um pedaço (se liga que agora a altura do triângulo é 1 e não mais 2, heim?)
Fazendo o somatório das forças em :
Em :
E para o momento:
Ufaaa... acabamos. Bora pra mais uma?