Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.9 - Ex. 7

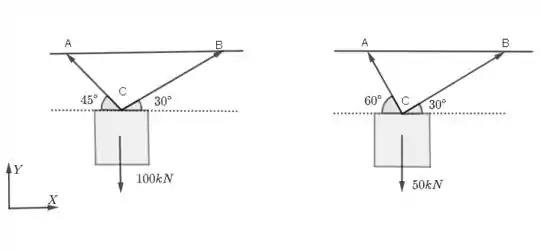
Determine os esforços nos cabos AC e BC que equilibram os corpos da figura seguinte

Passo 1

Na primeira figura, temos uma força peso F P → = - 100   k N   j ^ . O esforço AC pode ser decomposto como

F A C   X = - F A C   c o s 45   ° = - 0,707   F A C    

F A C   Y = F A C   s e n   45   ° = 0,707   F A C    

O esforço BC pode ser decomposto como

F B C   X = F B C   c o s 30   ° = 0,866   F B C    

F B C   Y = F B C   s e n   30   ° = 0,5   F B C    

Passo 2

Como as forças estão em equilíbrio, devemos ter

∑ F X = 0   ⇒ F A C   X + F B C   X = - 0,707   F A C   + 0,866   F B C   = 0   ⇒ F A C = 0,866 0,707   F B C

∑ F Y = 0   ⇒ F A C   Y + F B C   Y + F P = 0,707   F A C   + 0,5   F B C - 100   k N = 0

⇒ 0,707   F A C   + 0,5   F B C = 100   k N

A primeira equação de equilíbrio nos deu F A C em termos de F B C . Agora, substituímos essa relação na segunda equação de equilíbrio para encontrar F B C :

0,707   0,866 0,707   F B C   + 0,5   F B C = 0,866     F B C   + 0,5     F B C   = 1,366     F B C   = 100   k N

⇒   F B C   = 100   k N 1,366 ≈ 73,2   k N

Agora que sabemos o módulo de   F B C   , substituímos em   F A C   :

F A C = 0,866 0,707   F B C = 0,866 0,707 73,2   k N ≈ 89,7   k N  

Passo 3

O mesmo raciocínio vale para a figura 2. Temos F P → = - 50   k N   j ^ ,

F A C   X = - F A C   c o s 60   ° = - 0,5   F A C    

F A C   Y = F A C   s e n   60   ° = 0,866   F A C    

e

F B C   X = F B C   c o s 30   ° = 0,866   F B C    

F B C   Y = F B C   s e n   30   ° = 0,5   F B C    

Passo 4

A partir das equações de equilíbrio, obtemos

∑ F X = 0   ⇒ F A C   X + F B C   X = - 0,5   F A C   + 0,866   F B C   = 0   ⇒ F A C = 0,866 0,5   F B C = 1,732     F B C

∑ F Y = 0   ⇒ F A C   Y + F B C   Y + F P = 0,866   F A C   + 0,5   F B C - 50   k N = 0

⇒ 0,866   F A C   + 0,5   F B C = 50   k N

Como F A C = 1,732     F B C , então

0,866   F A C   + 0,5   F B C = 0,866   ⋅ 1,732     F B C   + 0,5   F B C ≈ 1,5   F B C + 0,5   F B C = 2   F B C =   50   k N

⇒ F B C = 50   k N 2 = 25   k N

Agora substituímos F B C = 25   k N em F A C :

F A C = 1,732     F B C = 1,732   ⋅ 25   k N = 43,3   k N

Resposta

Figura 1:   F B C   = 73,2   k N , F A C = 89,7   k N   .

Figura 2::   F B C   = 25   k N , F A C = 43,3   k N   .

Exercícios de Livros Relacionados

A barra esguia e uniforme de comprimento 3 r e massa m repousa contra a superfície circular, conforme mostrado. Determine a força normal no ponto de contato C e a magnitude da reação de pivô ideal em
Um mecânico está reinstalando uma lâmina recém-afiada em um cortador de grama. Um bloco de madeira encaixado em C impede a lâmina de girar quando a força de 30l b é aplicada ao cabo da chave. A lâmina
Um bloco colocado sob a cabeça do martelo de garra, conforme mostrado, facilita muito a extração do prego. Se um puxão de 50l b no cabo é necessário para puxar o prego, calcule a tensão T no prego e a
Por causa do carregamento de longo prazo da tensão de 900N na linha de energia, o poste de utilidades uniforme desenvolveu uma inclinação de 5 ° . Se a massa por unidade de comprimento do poste de 9m
O guindaste portátil da oficina automotiva está levantando um motor de 420l b . Para a posição mostrada, calcule a magnitude da força suportada pelo pino em C e a pressão do óleo P contra o pistão de