Enunciado
Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.9 - Ex. 8
Uma esfera de aço do raio de 5,0 cm está em repouso sobre dois anteparos inclinados como
mostra a parte esquerda da próxima figura. Com o conhecimento de que o peso específico do aço é . determine as forças que esses anteparos exercem sobre a esfera
Passo 1
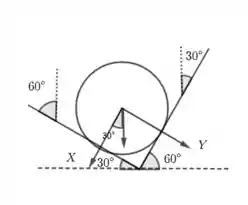
A maior dificuldade dessa questão é identificar um sistema de coordenadas conveniente e quais são os ângulos envolvidos. Para isso, vamos escolher o sistema de eixos como mostrado na figura. Desse modo, a força que o anteparo 1 exerce sobre a esfera será , pois essa força aponta no sentido negativo de . Da mesma forma, a força que o anteparo 2 exerce sobre a esfera será .
Passo 2
A esfera também sofre o efeito da força peso. Cada pequena seção da esfera sofrerá a ação da força peso, mas o efeito sobre toda a esfera é equivalente a ter uma força de módulo , com origem no centro da esfera. Não sabemos qual a massa da esfera, mas sabemos seu peso específico (ou seja, seu peso por unidade de volume) e raio. Para obter o peso da esfera, basta multiplicar o peso específico pelo volume da esfera. Para tanto,, podemos utilizar a fórmula do volume de uma esfera de raio , que é
O raio da esfera é , mas vamos converter esse valor para metros porque o peso específico é dado em . Então, . Substituindo esse valor na fórmula do volume, obtemos
Logo, o peso da esfera é, em módulo
No nosso sistema de coordenadas, a força peso tem componentes em e . Para calcular essas componentes, devemos descobrir o ângulo entre a força peso e . Na segunda figura, vemos que esse ângulo é . Assim,
Passo 3
Agora que identificamos todas as forças, podemos usar as equações de equilíbrio e determinar e :