Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 3.Problemas - Ex. 31
Por causa do carregamento de longo prazo da tensão de na linha de energia, o poste de utilidades uniforme desenvolveu uma inclinação de . Se a massa por unidade de comprimento do poste de for e a massa do suporte da lâmpada for insignificante, determine as reações no suporte de solo .
Passo 1
Fala galera! Tudo certo? Vamos dividir a resolução em algumas etapas, beleza? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar as reações de apoio em do poste engastado que sofreu uma inclinação de em relação à vertical devido à tensão de nos cabos. O poste possui peso dado por:
Para entender melhor a disposição dos carregamentos, vamos fazer o diagrama de corpo livre do sistema:
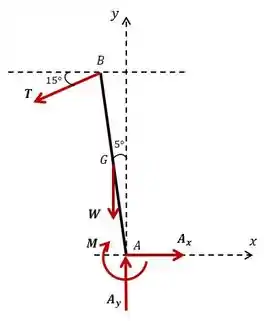
Antes dos nossos cálculos de fato, vamos definir algumas variáveis.
A distância entre o ponto e o eixo :
A distância entre o ponto e o eixo :
A altura entre o ponto e o eixo :
Passo 2
Show, feito isso, ainda temos três incógnitas para encontrar: as reações , e . Para isso vamos utilizar as equações de equilíbrio. Por convenção, vamos considerar as forças como positivas quando elas estiverem no sentido positivo dos eixos e os momentos positivos quando estiverem no sentido anti-horário.
Começando pelo momento em torno de , já que isso elimina duas das nossas incógnitas.
Passo 3
Show! Agora faremos o somatório de forças na direção para encontrar :
E na direção para encontrar :
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 