Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 9

9. Resolva o Problema 9.6 usando as equações de transformação de tensão desenvolvidas na Seção 9.2. Moste o resultado em um desenho.

Passo 1

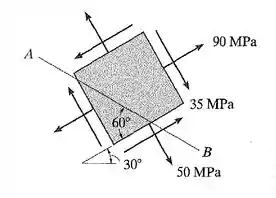
Olhando a figura do enunciado, tiramos no estado plano de tensão, que:

, tensão normal de tração

, com valor negativo, uma vez que as setas de tensão cisalhante estão apontando para o primeiro e terceiro quadrantes

, é o ângulo do plano inclinado com a horizontal

, é o ângulo do plano inclinado com a vertical, considerando o sentido anti-horário como positivo. E é esse ângulo, que vamos utilizar em nossos cálculos.

Passo 2

Agora, vamos aplicar as equações de transformação de tensão para determinar o valor de , e .

Sabemos que é dado em função das tensões normais e e da tensão cisalhante , pela seguinte fórmula:

Substituímos então, os valores numéricos pertinentes a cada variável:

E conhecemos também, a fórmula do nosso , que tem o seguinte aspecto:

Substituímos o valor de cada variável:

Por fim, falta apenas usar a fórmula para encontrar a tensão cisalhante , que tem a seguinte cara:

E substituindo os valores numéricos adequados, chega-se a:

Pronto! Encontramos as nossas tensões no elemento orientado de com a vertical.

Passo 3

E as nossas novas tensões, vão estar dispostas de acordo com a seguinte imagem, sem os valores numéricos, é claro, por se tratar de uma representação.

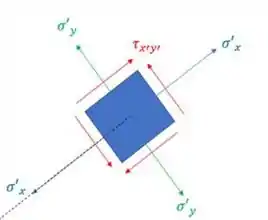
e tem a direção descrita na imagem, porque são trações compressivas. Já o valor obtido para foi negativo, por isso as setas de tensão cisalhantes convergem para o segundo e quarto quadrantes, como na figura acima.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5. O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes de tensão que agem no plano inclinado A B . Resolva o problema usando o método do equilíbri

Determine o estado de tensão equivalente, se um elemento estiver orientado a 40º em sentido horário em relação ao elemento mostrado. Use o círculo de Mohr.

O estado de tensão num ponto um membro é mostrada no elemento. Determinar os componentes de tensão que actuam sobre o plano inclinado AB.

O vaso de pressão cilíndrico tem raio interno de 1,25m e espessura de parede de 15m m . É feito de chapas de aço soldadas ao longo de uma linha de junção a 45 ° em relação à horizontal. Determine as c

Determine o estado de tensão equivalente em um elemento se ele estiver orientado a 30º em sentido horário em relação ao elemento mostrado. Use as equações de transformação de tensão.