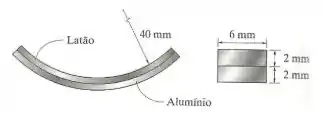
Uma tira bimetálica é feita de pedaços de alumínio 2014-T6 e latão vermelho C83400 e tem a seção transversal mostrada na figura. Um aumento na temperatura provoca a curvatura de sua superfície neutra e forma um arco circular com raio de 400 mm. Determine o momento que agiria em sua seção transversal resultante de sua tensão térmica. Eal = 74 GPa e Elat = 102 GPa.
Passo 1
Faaaala, meu povo bonito!! Tudo bem com vocês?? A nossa questão de hoje nos traz uma tira composta por dois materiais diferentes, mas vou te explicar direitinho. Os materiais que compõem são o alumínio e o latão, e ele nos pede para calcular os dois momentos fletores máximas (tanto para o alumínio quanto para o latão) e pegaremos o menor (afinal, se pegarmos o maior, o ‘’mais fraco’’ vai se romper com o momento do outro) para depois da deformação térmica. Viu?? Ela só tem cara de malvada, mas vamos resolver rapidinho. Vem comigo!!
Passo 2
A primeira coisa que precisamos achar é a relação entre os coeficientes Elat e Eal e o novo comprimento da viga.
![]()
![]()
n = = 0,7255
b’ = nb = 0,7255 x 6 = 4,353 mm
Agora que sabemos o comprimento e a altura de cada um dos nossos elementos da viga, vamos descobrir nosso ycc
ycc = mm
Passo 3
Agora que já temos nossas dimensões, podemos calcular o momento máximo da viga. Para isso, vamos calcular primeiro o nosso I, para só depois substituir na nossa formulinha.
I =
I = 2,708378 x 10-11 m4
ρ = 400 + (4-2,1591) = 401,84 mm
ρ =
M = 6,87 N.m
Resposta
M = 6,87 N.m