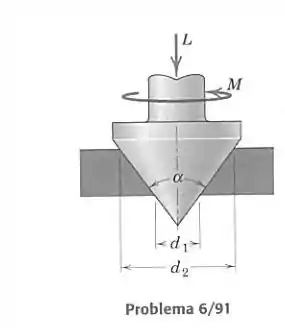
Determine a expressão para o torque necessário para girar o eixo cuja pressão axial é sustentada por um mancal cômico. O coeficiente de atrito é , e a pressão no mancal é constante.
Passo 1
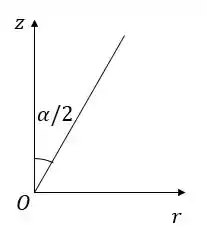
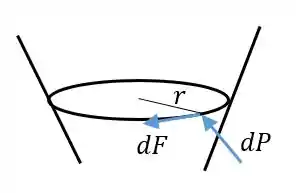
Aqui devemos encontrar a expressão do momento infinitesimal em cada parte da superfície cônica, e então integrar. Vamos separar a superfície de contato em círculos de raio . A altura em relação à ponta do formato cônico é função de . Em cada círculo, atuará uma força normal total e uma força de atrito total .
Passo 2
Em cada círculo, temos forças normais aplicadas, e forças de atrito que impedem o giro iguais a . Então o momento feito em torno do eixo central é
Além disso, cada força é igual à pressão , que tem valor desconhecido, vezes a área :
Então:
Mas a área é a área de uma circunferência de raio e espessura .
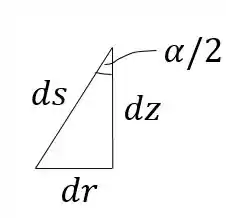
A espessura pode ser colocada em função de :
Então a área infinitesimal é:
Colocando em função de o momento é então:
Passo 3
Temos então a expressão de em função de r, mas ela não está completa, pois não sabemos qual é o valor de . Devemos então achar esse valor fazendo o equilíbrio vertical da peça, pois a carga aplicada deve ser igual à integral das componentes verticais das forças . Essas forças tem inclinação de em relação à horizontal, então a componente vertical é:
Substituindo pelo valor de em função de :
Agora integramos, com indo de a :
Então temos a pressão em função de :
Passo 4
Agora, substituindo , temos só em função de nosso momento atuando em cada círculo:
Integramos essa expressão de a , para finalmente encontrar o momento total :
Esse é o momento total causado pelo atrito, e também o momento que deve ser feito para se opor a ele e fazer girar a peça.