Determine o ângulo entre a horizontal e a rampa mais inclinada que o veículo do Prob. 6/87 pode suportar sem rolar por si próprio na ausência de uma força . Considere que o coeficiente de atrito nos mancais das rodas vale 0,20.
Passo 1
Agora, como o carro está parado num plano inclinado, as forças realizadas pelo solo nas quatro rodas devem equilibrar o peso total do carro, então as forças realizadas pelo solo são verticais e iguais a um quarto do peso do carro. O peso do carro é 480 kg, então a força do solo em cada roda é:
Além dessa força temos também o peso de cada roda, aplicado em seus centros. A roda tem massa de 20 kg então o peso é:
Finalmente, temos a força aplicada pelo eixo no mancal da roda, que faz um ângulo com a superfície de contato entre os dois corpos, tal que:
Sendo o coeficiente de atrito entre o mancal e o eixo. Essa força também deve ser vertical, pois todas as outras são e o carro está em equilíbrio. Representamos então o diagrama de corpo livre da roda:
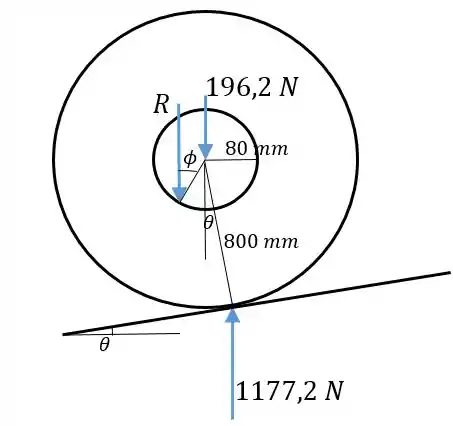
Passo 2
Pelo equilíbrio vertical das forças, achamos :
Agora fazendo o momento em torno do centro ser zero: