Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 73
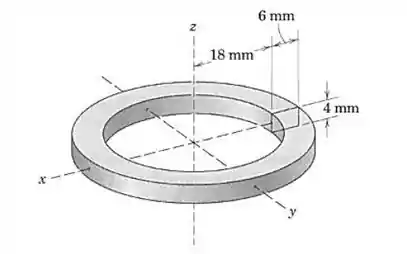
Usando os métodos desta seção determine a área superficial A e o volume V do corpo formado pela revolução da área retangular por 360° em torno do eixo z.
Passo 1
FALA AÍ MEU CONSAGRADO, bora resolver essa questão, usaremos o Teorema de Pappus para resolvê-la, assim como o enunciado pede, vida de estudante é triste, mas coloca essa tristeza de lado e vem ver as equações que usaremos para o calculo da área superficial A e o volume V do corpo:
(1)
(2)
O seria o ângulo de revolução em torno do eixo z (fornecido no enunciado) , o seria a distância entre o eixo z e o centro de massa do corpo, o L seria o perímetro da secção do corpo e o A seria a área, meu consagrado, se você não sabia disso, ENTÃO SAIA DAQUI, não estou te expulsando, mas convidando para ver o conteúdo de centro de massa disponível no Respode aí, estuda lá e depois volta, CONTINUANDO...
Passo 2
Analisando a figura, conseguimos determinar que o centro de massa daquela secção equivale à 3mm, REPITINDO, se você não sabe o porquê do centro de massa ser 3mm, SAIA DAQUI e vê o conteúdo do Responde aí relacionado com centro de massa, CONTINUANDO....somando a distância do centro de massa com a distância do corpo em relação ao eixo z obtemos o valor de 21mm, valor esse que seria o nosso , com isso, basta calcular o comprimento da secção, que equivale a soma de todos os lados, logo 6+4+4+6 = 20, agora temos as variáveis necessárias para o calculo da área:
Para o calculo do volume a única alteração que faremos, meu bom, é trocar o comprimento pela área da secção, que equivale a 6 * 4 = 24, com isso, basta aplicar os dados obtidos na fórmula:
PRONTINHO, vemos que é apenas uma aplicação do teorema de Pappus, portanto, não há o que temer, por hoje é só pessoal, ATÉ MAIS!