Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 111
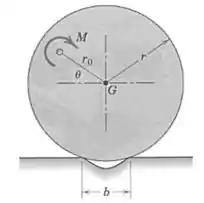
Uma roda com massa e raio , com centro de massa no seu centro geométrico, está apoiada em uma pequena depressão com largura . Determine o momento mínimo aplicado à roda na posição mostrada, de forma a rolar a roda para fora da depressão. Assuma que não existe deslizamento. Quais são as influências de , e ?
Passo 1
Vamos pensar nos momentos que agem sobre a roda. Além do momento que age na posição em relação ao centro geométrico da roda, temos a força peso agindo nesse centro e as forças de contato nas bordas da depressão.
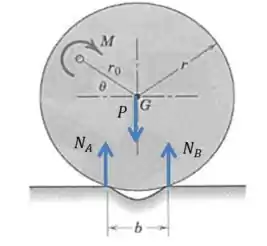
Agora imagine o seguinte, quando a roda está prestes a rolar para fora da depressão ela perde o contato com o ponto :
E então ficamos apenas com as forças e e o momento .
Passo 2
Como não conhecemos a força , e nosso objetivo é calcular , vamos montar uma equação de equilíbrio dos momentos em relação ao ponto :
Os únicos momentos são o , e o gerado por , que está a uma distância perpendicular do ponto :
E a última pergunta é sobre as influências de , e . Pela equação que escrevemos, claramente nenhuma dessas variáveis aparece no cálculo do momento.
Resposta
O momento mínimo é , que não depende de , e nem .