Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.3 - Ex. 50
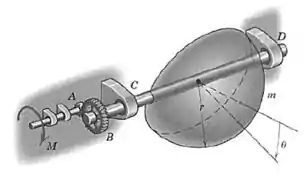
Determine o momento que deve ser aplicado ao eixo de forma a manter o hemisfério homogêneo em uma posição angular arbitrária, medida pelo ângulo . Os raios das engrenagens , e do hemisfério são , , , respectivamente. Assuma que o atrito em todos os mancais é desprezível.
Passo 1
Perceba que o momento age sobre um eixo que faz a engrenagem girar, e essa engrenagem transmite o movimento para a engrenagem , e essa sim está presa ao hemisfério.
O problema todo aqui é “segurar” o peso do hemisfério. Se olharmos a tabela no final do livro, vamos ver que o centro de massa de um hemisfério homogêneo está na seguinte posição:
Vamos representar isso no desenho:
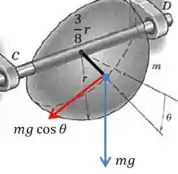
E então o momento gerado pela força peso em relação à engrenagem é:
Onde o sinal negativo aparece porque esse momento favorece a rotação no sentido horário.
Passo 2
Se queremos o equilíbrio dos momentos na engrenagem , a força que a engrenagem faz sobre ela tem que gerar um momento igual ao gerado pela força peso.
Se o raio da engrenagem é essa equação de equilíbrio vai ficar assim:
E isolando a força :
Passo 3
Beleza, já descobrimos a força que a engrenagem tem que exercer sobre a . Agora vamos exigir que o momento gerado por essa força no primeiro eixo seja igual ao momento representado na imagem:
Como o raio da engrenagem é :
E então o momento é:
Resposta
O momento deve ser .