Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 120

Determine os componentes x , y e z da força F que atua no tetraedro como mostrado. Os valores de a , b e c e F são conhecidos e M é o ponto médio da aresta A B .

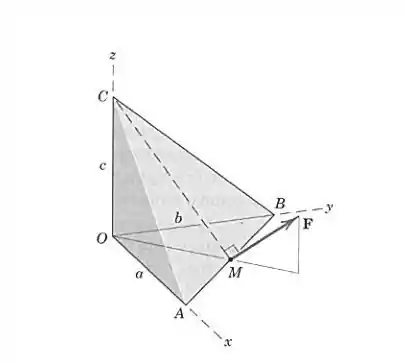
Passo 1

O que queremos fazer aqui é decompor F em componentes x , y e z , encontrando o seno e cosseno do ângulo ϕ que a linha de força faz com o plano x y e do ângulo θ que a projeção da força no plano x y faz com o eixo x . Então poderemos calcular da seguinte forma:

F z = F sen ⁡ ϕ

F y = F cos ⁡ ϕ sen ⁡ θ

F x = F cos ⁡ ϕ cos ⁡ θ

Passo 2

O ângulo θ que a gente quer é o ângulo A O ^ M . Para encontrar o ângulo ϕ que está entre F e o plano x y podemos observar que ele é igual ao ângulo O C ^ M , pois:

ϕ + 90 + O M ^ C = 180 ⇒ ϕ = 90 - O M ^ C

E pelo triângulo O C M a soma dos ângulos internos deve ser 180 ° :

O C ^ M + O M ^ C + 90 = 180 ⇒ O C ^ M = 90 - O M ^ C = ϕ

Então devemos achar o seno e o cosseno dos ângulo   A O ^ M e O C ^ M .

Passo 3

Pra achar θ = A O ^ M , vamos dar uma olhada melhor no triângulo O A B :

Uma regrinha muito importante que acabamos de usar é a de que em um triângulo retângulo a mediana que vai do vértice do ângulo reto até a hipotenusa tem o valor da metade da hipotenusa. Agora já podemos achar o seno e o cosseno de θ :

A B - = 2 d = a 2 + b 2

sen ⁡ θ = b A B - = b a 2 + b 2

cos ⁡ θ = a a 2 + b 2

Passo 4

Agora devemos achar sen ⁡ ϕ e cos ⁡ ϕ . Devemos então aplicar Pitágoras no triângulo O C M para encontrar o tamanho do lado C M - . Já sabemos que O M - = d = a 2 + b 2 / 2 , então:

C M - 2 = c 2 + d 2 = c 2 + a 2 + b 2 2 2 = a 2 + b 2 + 4 c 2 4

C M - = a 2 + b 2 + 4 c 2 2

Agora temos:

sen ⁡ ϕ = O M - C M - = a 2 + b 2 a 2 + b 2 + 4 c 2 2 = a 2 + b 2 a 2 + b 2 + 4 c 2

cos ⁡ ϕ = c C M - = c a 2 + b 2 + 4 c 2 2 = 2 c a 2 + b 2 + 4 c 2

Passo 5

Agora já podemos calcular as componentes de F:

F z = F sen ⁡ ϕ = F a 2 + b 2 a 2 + b 2 + 4 c 2

F y = F cos ⁡ ϕ sen ⁡ θ = 2 b c F a 2 + b 2 a 2 + b 2 + 4 c 2

F x = F cos ⁡ ϕ cos ⁡ θ = 2 a c F a 2 + b 2 a 2 + b 2 + 4 c 2

Resposta

F x = 2 a c F a 2 + b 2 a 2 + b 2 + 4 c 2

F y = 2 b c F a 2 + b 2 a 2 + b 2 + 4 c 2

F z = F a 2 + b 2 a 2 + b 2 + 4 c 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a intensidade e os ângulos diretores  coordenados da força F que atua sobre o suporte. A  componente de F no plano x–y é 7kN.
Determine a intensidade e os ângulos diretores coordenados de F3, de modo que a resultante das três forças atue ao longo do eixo y positivo e tenha uma intensidade de 600 N.
Determine a intensidade e os ângulos diretores coordenados de F3, de modo que a resultante das três forças seja zero.
Determine a intensidade e os ângulos diretores  coordenados da força resultante, e desenhe esse vetor no sistema de coordenadas.
O parafuso está submetido à força F, que tem componentes atuando ao longo dos eixos x, y, z, como mostra a figura. Se a intensidade de F é 80N, α= 60 ° e γ= 45 ° , determine as intensidades de suas co