Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 6
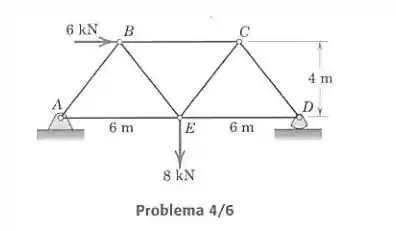
Determine a força em cada elemento da treliça carregada.
Passo 1
Vamos calcular as forças pelo método dos nós, isolando cada pino da treliça. Primeiro vamos às equações externas da treliça, para acharmos os valores de reação de e . Note que o apoio em só causa uma reação para cima:
Para achar fazemos o momento em torno de :
Então encontramos :
Passo 2
Agora vamos calcular as equações para cada nó. indica que a força traciona a barra (aponta pra fora do nó) e indica que a força comprime a barra (aponta para o nó). Se o sinal de uma força der negativo quer dizer que erramos seu sentido.
Nó A:
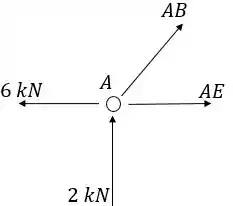
O ângulo entre e tem seno e cosseno .
O sinal negativo indica que erramos o sentido e na verdade é de compressão. Agora achamos :
Passo 3
Nó B:
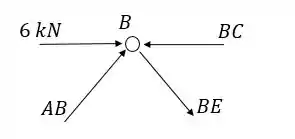
Isolando e substituindo :
Então:
Passo 4
Nó E:
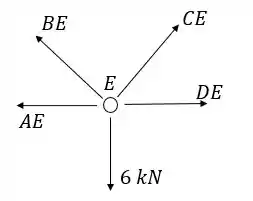
Substituindo os valores:
Dividimos tudo por então
Agora encontramos :
Passo 5
Nó D:
Só precisamos da equação das forças verticais para encontrar :