Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.3 - Ex. 25

A caçamba do caminhão de entrega de alimentos para aeronaves tem massa m quando carregada e é levantada pela aplicação de um torque M na extremidade inferior da engrenagem, que é articulada com a estrutura do caminhão. Os rasgos horizontais permitem que estrutura articulada se desdobre à medida que a caçamba é elevada. Expresse M em função de h .

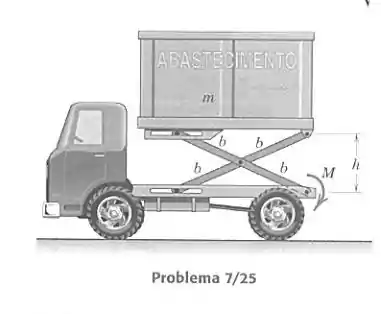
Passo 1

Vamos considerar como nosso sistema a caçamba e as barras em X. Utilizando o Princípio do Trabalho Virtual, se o sistema está em equilíbrio o trabalho virtual δ U total realizado pelas forças externas ativas (forças que realizam trabalho) para um deslocamento pequeno do sistema deve ser zero:

δ U = 0

Os nossos agentes externos ativos são o peso m g da caçamba e o momento M . As forças nos apoios não realizam trabalho, pois os da direita são fixos e os da esquerda fazem apenas força vertical, enquanto o movimento neles só pode ser horizontal. Vamos calcular então o trabalho realizado pelo peso m g da caçamba e pelo momento M para uma variação virtual δ h da altura h , e então aplicar o Princípio do Trabalho Virtual.

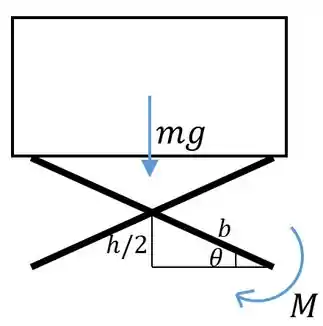
Passo 2

Primeiro calculamos rapidamente o trabalho δ U 1 feito pelo peso da caçamba em função de δ h . Para uma variação positiva da altura temos um trabalho negativo do peso, dado por:

δ U 1 = - P   δ h = - m g   δ h

Passo 3

Agora calculamos o trabalho δ U 2 realizado pelo momento. O trabalho do momento é:

δ U 2 = M δ θ

O momento é positivo, pois um aumento de θ gira a barra no sentido horário, mesmo sentido do momento. Devemos então relacionar a variação δ θ do ângulo com a variação δ h da altura. Pelo triângulo da figura, temos:

sen ⁡ θ = h 2 b

Derivando os dois lados:

cos ⁡ θ δ θ = δ h 2 b

Então:

δ θ = 1 2 b cos ⁡ θ δ h

O trabalho é então:

δ U 2 = M δ θ = M 2 b cos ⁡ θ δ h

Passo 4

Pelo Princípio do Trabalho Virtual, temos então:

δ U = δ U 1 + δ U 2 = 0

⇒ - m g   δ h + M 2 b cos ⁡ θ δ h = 0

⇒ M 2 b cos ⁡ θ δ h = m g   δ h

Cortando δ h , chegamos ao valor de M :

M = 2 m g b cos ⁡ θ

Mas o valor de θ , não é dado pelo enunciado, precisamos colocar em função de h e b . Já sabemos que sen ⁡ θ = h / 2 b . Agora usamos a relação fundamental trigonométrica:

sen 2 ⁡ θ + cos 2 ⁡ θ = 1

⇒ cos ⁡ θ = 1 - sen 2 ⁡ θ

Substituindo o valor de sem ⁡ θ :

cos ⁡ θ = 1 - h 2 b 2

Então, finalmente temos o valor de M :

M = 2 m g b 1 - h 2 b 2

Resposta

M = 2 m g b 1 - h 2 b 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

71- O painel retangular uniforme de massa m e centro de massa em G é guiado por roletes- o par superior na guia horizontal e o par inferior na guia vertical. Determine a força P , aplicada a extremida
72- O disco uniforme de alumínio com raio R e massa m rola sem deslizar sobre a superfície circular fixa de raio 2 R . Um cilindro de chumbo também de massa m está preso ao disco e seu centro está loc
76- Determine o ângulo θ para haver equilíbrio da conexão uniforme de 10k g e centro de massa em G , a medida que sua posição no plano vertical é influenciada pela força horizontal de 80N aplicada a s
75- A barra O A , que tem uma massa de 25k g e centro de massa em G , é articulada em torno de sua extremidade O e balança no plano vertical sob a restrição do contrapeso de 10k g . Escreva a expressã
77- A figura mostra a vista lateral de uma janela de ventilação de 10k g e centro de massa em G , articulada em relação a um eixo horizontal que passa por sua aresta em O . Quando θ = 90 , a mola de r