A treliça é fabricada usando membros que têm um peso de . Remova as forças externas da treliça e determine a força em cada membro devido ao peso dos membros. Indique se os membros estão sob tração ou compressão. Considere que a força total que atua sobre um nó é a soma da metade do peso de todos os membros conectados ao nó.
Passo 1
O problema que que a gente encontre a força de cada membro mostrando se ele está sendo tracionada ou comprimida.
Vamos começar encontrando as forças que estão atuando nas extremidades devido ao peso como diz no problema:
A força aplicada em cada junta é o peso da metade de cada barra conectada na junta.
Tendo isso, vamos usar agora o momento considerando o ponto como eixo de rotação para descobrirmos a força atuante na junta :
Assim, a gente encontra:
Analisando a estrutura geometricamento notamos que a melhor ordem de analisar as juntas é:
Então, vamos começar pelas forças da junta , porque tem apenas duas forças desconhecidas e possui uma que o problema deu. Sabendo que o somatório das forças no eixo e somatório das forças do eixo é , pois a estrutura encontra-se em equilíbrio.
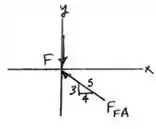
No eixo primeiro:
Assim encontramos:
Estando sob compressão.
Agora no eixo :
Então encontramos:
Nesse caso, estando sob tração.
Passo 2
Agora, vamos analisar as forças da junta , sabendo que o somatório das forças no eixo e somatório das forças do eixo é , pois a estrutura encontra-se em equilíbrio.
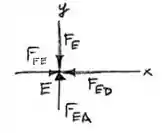
No eixo primeiro:
Assim encontramos:
Estando sob tração.
Agora no eixo :
Então encontramos:
Nesse caso, estando sob compressão.
Passo 3
Agora você analisa as juntas , e . Os diagramas de corpo livre são:
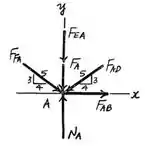
Assim você vai encontrar as forças:
(Compressão)
(Tração)
(Tração)
(Tração)
(Compressão)
Resposta
(Compressão)
(Tração)
(Tração)
(Compressão)
(Compressão)
(Tração)
(Tração)
(Tração)
(Compressão)