Determine a maior força que pode ser aplicada à treliça de modo que nenhum dos membros esteja sujeito a uma força maior que em tração ou em compressão.

O problema que que a gente encontre a maior força que pode ser aplicada em , de forma que não ultrapasse em tração ou em compressão. Nesse caso, vamos analisar junta por junta (Método dos nós).

Observando as treliças e a estrutura completa notamos que a melhor ordem para analisar cada junta é:

Também percebemos que boa parte dos ângulos formados na estrutura são de e .

Pra isso, você faz esse calculo:

Então, vamos começar pelas forças da junta . Sabendo que o somatório das forças no eixo e somatório das forças do eixo é , pois a estrutura encontra-se em equilíbrio.

No eixo primeiro:

Assim encontramos:

Estando sob Tração.

Agora no eixo :

Então encontramos:

Nesse caso, estando sob compressão.

Agora, vamos analisar as forças da junta , sabendo que o somatório das forças no eixo e somatório das forças do eixo é , pois a estrutura encontra-se em equilíbrio.

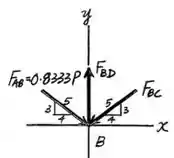
No eixo primeiro:

Assim encontramos:

Estando sob compressão.

Agora no eixo :

Então encontramos:

Nesse caso então, estando sob tração.

Faça o mesmo na junta , e você obterá:

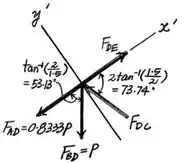
(Compressão)

(Tração)