Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.3 - Ex. 1

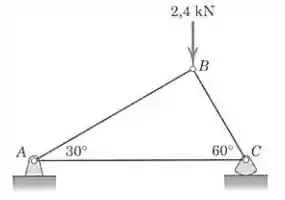
Determine a força em cada elemento da treliça carregada. Explique por que não é necessário conhecer o comprimento dos elementos.

Passo 1

Considerando o nó B , obtemos duas equações, pelo equilíbrio em x e em y , respectivamente:

A B cos ⁡ 30 ° = B C cos ⁡ 60 °

A B   s e n   30 ° + B C   s e n   60 ° = 2,4   k N

Logo,

A B = 1,2   k N   C

B C = 2,08   k N   C

Passo 2

Agora, consideramos o equilíbrio em x para o nó C :

- A C + B C cos ⁡ 60 ° = 0

A C = 1,039   k N   T

Resposta

A B = 1,2   k N   C

A C = 1,039   k N   T

B C = 2,08   k N   C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a força no elemento A C da treliça carregada. Os dois elementos com formato de ¼ de círculo atuam como elementos de duas forças.
Cada elemento da treliça é uma barra uniforme de 8 m pesando 400 kg. Calcule a tração ou compressão média em cada elemento, devida aos pesos dos elementos.
A treliça é formada por triângulos de lado a e está carregada e apoiada como mostrado. Determine as forças nos elementos E F , D E e D F .
Determine as forças nos elementos B C e B G da treliça carregada.
Uma ponte levadiça está sendo levantada por um cabo E I . As quatro cargas mostradas nos nós são devidas ao peso do pavimento. Determine as forças nos elementos E F , D E , D F , C D e F G .