Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 94
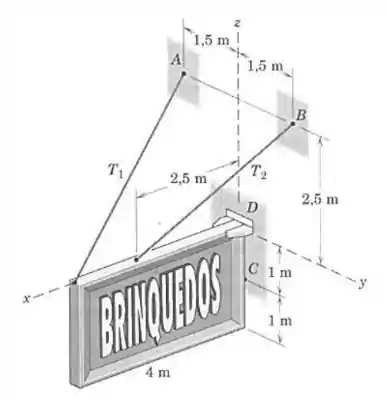
Um letreiro retangular sobre uma loja tem uma massa de e seu centro de massa está no centro do retângulo. A sustentação contra a parede no ponto pode ser considerada como uma rótula. Na extremidade a sustentação é dada apenas na direção . Calcule as forças trativas e nos arames de sustentação, a força total em e a força lateral em .
Passo 1
Vamos começar escrevendo as forças e em forma vetorial. Para isso precisamos dos vetores unitários nas direções de e :
Além dessas duas forças, e do peso da placa, temos também uma força agindo apenas na direção do eixo no ponto (conforme o enunciado), e uma força que apoia a placa contra a parede, e tem componentes e . Queremos calcular todas essas forças.
Passo 2
Vamos começar analisando o equilíbrio dos momentos em relação ao eixo :
Essa foi uma boa escolha de eixos porque anulou os momentos gerados pelas duas tensões, por e pela outra componente da força .
Agora vamos tomar um eixo que exclua todas as forças exceto as duas tensões, o eixo . Como temos que lidar com esse momento em três dimensões, precisamos escrever os vetores-posição que ligam os pontos de aplicação das tensões ao eixo :
E basta resolver os produtos vetorais pegando apenas a componente em
E então:
Passo 3
Agora vamos analisar o equilíbrio das forças na direção do eixo :
E substituindo o resultado anterior nessa equação:
E substituindo isso em qualquer uma das equações de cima encontramos:
Passo 4
Agora que conhecemos os módulos das duas tensões, vamos analisar o equilíbrio das forças nas direções dos outros eixos:
Isso quer dizer que a força aponta no sentido negativo do eixo .
E por fim vamos considerar o equilíbrio das forças no eixo (cuidado com a confusão entre e !):
E jutando essa informação com o que cálculamos lá em cima:
Resposta
As forças são , , e ;