Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 6.Problemas - Ex. 19

Determine a força em cada um dos elementos localizados à esquerda do elemento FG para a treliça de telhado em tesoura mostrada na figura. Indique se cada elemento está sob tração ou sob compressão.

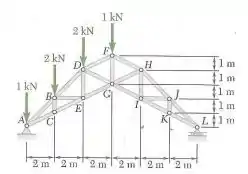
Passo 1

Falai moçadinha, show de bolinhas??

Bora la??

Aplicando Somatório de momento em x

∑ F x = 0 ;

A x = 0

+ ↺   ∑ M I = 0 ;

1   k N 12   m + 2   k N 10   m + 2   k N 8   m + 1   k N 6   m - A y 12   m = 0

12   A y = 54

A y = 4.50   k N   ↑

Nos podemos notar que no membro BC a força e 0

F B C = 0

Passo 2

Temos

F C E = F A C

Ponto A

→ + ∑ F x = 0 ;

1 2 F A B + 2 5 F A C = 0             ( 2 )

+ ↑ ∑ F y = 0

1 2 F A B + 2 5 F A C + 3.50   k N                   ( 3 )

D.C.L

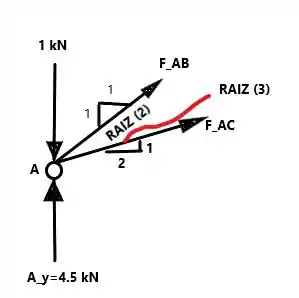
Multiplicando (3) e (2) por (2)

- 1 2 F A B - 7 k N = 0

F A B = 9.90 k N     ( C )

Passo 3

Subtraindo (3) por (2)

1 5 F A C - 3.50   k N = 0

F A C = 7.826   k N       ( T )

F C E = 7.83   ( T )

Aplicando somatório das forças em B

+ ↑ ∑ F y 0 ;

1 2 F B D + 1 2 9.90   k N - 2   k N = 0

F B D = - 7.071   k N  

F B D = 7.07   k N   ( C )

→ + ∑ F x = 0 ;

F B E + 1 2 9.90 - 7.07 = 0    

F B E = - 2.000   k N  

F B E = 2.00   k N     ( C )

→ + ∑ F x = 0 ;

2 5 F E G - 7.826   k N + 2.00   k N = 0

F E G = 5.590   k N

F E G = 5.59   k N   ( T )

+ ↑ ∑ F y 0 ;

F D E - 1 5 7.826 - 5.590 k N = 0

F D E = 1.000   k N

F D E = 1.00   k N     ( T )

Passo 4

Ponto D

→ + ∑ F x = 0 ;

2 5 F D F - F D G + 1 2 7.071   k N = 0

F D F + F D G = - 5.590   k N           ( 4 )

+ ↑ ∑ F y 0 ;

1 5 F D F + F D G + 1 2 7.071   k N = 2   k N - 1 k N = 0

F D F + F D G = - 4.472     k N

2 F D F = - 10.062   k N

2 F D G = - 1.1180   k N

F D F = 5.03   k N     C

F D G = 0.559     k N     ( C )

Resposta

Vide o passo a passo

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as forças nos elemento D E e D L .
Determine as forças nos elementos B C e F G da treliça simétrica carregada. Mostre que esse cálculo pode ser realizado usando uma seção e duas equações, cada uma das quais contendo apenas uma das duas
Determine a força no elemento A E da treliça carregada.
Determine a força no elemento D G da treliça carregada.
Calcule as forças nos elementos B C , C D e C G da treliça carregada, formada por triângulos equiláteros, com lados de 8 m de comprimento.