Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 37
Determine a força no elemento da treliça carregada.
Passo 1
Vamos calcular as forças pelo método das seções em um trecho da treliça, e depois resolveremos as equações para o nó G. Vamos traçar uma seção passando por , e e considerar a parte da esquerda como se fosse um corpo rígido. Nosso desenho fica assim:
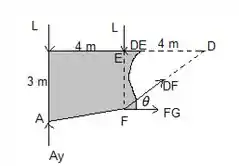
Passo 2
Precisamos da força para acharmos , que é a única que nos interessa no desenho pois está no nó . Achams calculando o momento em torno de para a treliça inteira:
Passo 3
Agora devemos achar . Repare que se fizermos o momento em torno de as forças desconhecidas e não entram na equação, então achamos diretamente:
Passo 4
Agora calculamos as equações de equilíbrio no nó . Precisamos do ângulo entre e a horizontal:
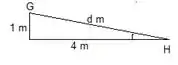
Por Pitágoras encontramos e então o seno e cosseno de
Agora calculamos as equações. Para as forças horizontais:
Substituindo :
Agora para as forças verticais:
Substituindo o seno: