Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 62
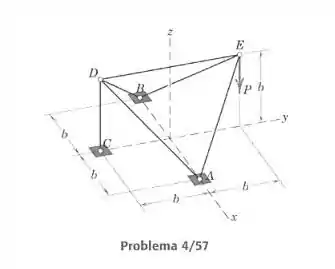
A treliça espacial com a forma de um tetraedro está sustentada por conexões articuladas nos pontos e na sua base e está impedida de girar em torno de pela barra vertical de amarração . Após escrever as componentes de reação verticais sob a treliça simétrica, em e , desenhe um diagrama de corpo livre da configuração triangular dos elementos e determine a componente da força exercida pela fundação da treliça em .
Passo 1
Pela simetria da treliça, descobrimos facilmente a tração na barra :
Agora realizando uma equação do momento em relação ao eixo que passa por e é paralelo a , devemos achar o valor da força vertical em .
Passo 2
As distâncias do eixo para os pontos são:
Então fazemos o momento total ser igual a zero, colocando negativos os momentos no sentido horário:
Agora achamos :
Pela simetria:
Passo 3
Agora vamos tratar o triângulo como se fosse um único corpo, e desenhar as forças atuantes nele:
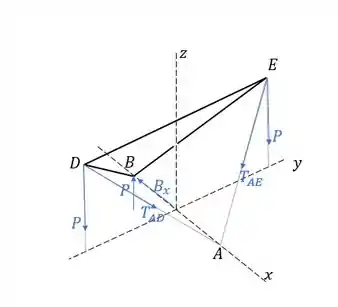
Existem forças desconhecidas em e . Podemos evitá-las calculando o momento total em torno do eixo :