Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 1

Determine a força em cada membro da treliça e indique se os membros estão sob tração ou compressão.

Passo 1

O problema quer que a gente encontre a força de cada treliça mostrando se ele está sendo tracionada ou comprimida.

Vamos começar procurando os membros de força zero (se existem), lembra das regrinhas? Vou te lembrar:

Caso existam duas barras colineares e uma terceira conectada, essa terceira barra é um membro de força zero:

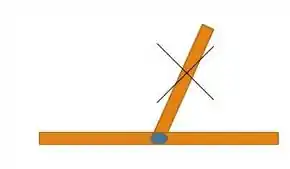
Repara que isso acontece com a barra E C . Ela está ligada em um nó que tem duas barras colineares. Então F E C = 0 .

Caso exista uma barra colinear a uma força e uma segunda barra conectada, essa barra é um membro de força zero:

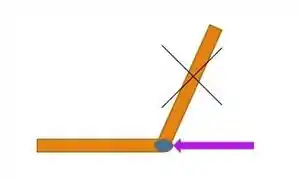
Caso haja um nó na extremidade, e nesse nó exista apenas duas barras chegando, essas duas barras são membros força zero, a não ser que exista forças atuando sobre o nó. Membros força zero:

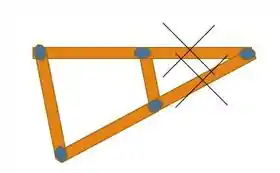
Por F E C ser uma força zero, acontece que F D C = F C B . Já que elas são colineares e não há interferências no nó entre elas. Vamos seguir!

Passo 2

Agora, vamos analisar as forças da junta D . Sabemos que o somatório das forças no eixo y e somatório das forças do eixo x é 0 , pois a estrutura encontra-se em equilíbrio.

No eixo x :

∑ F x = 0

600 - F E D ⋅ s e n 0 ° - F D C ⋅ E C _ D B _ = 0

600 - 0 - F D C ⋅ 2 4 2 + 2 2 = 0

Assim encontramos:

F D C = 1341,64   N ≈ 1,34   k N

Lembre que no passo 1 a gente descobriu que: F D C = F C B ? Agora é útil.

F D C = F C B = 1,34   k N

Que por fazerem uma força de reação nesse sentido, estão sob compressão.

Agora no eixo y :

∑ F y = 0

600 ⋅ c o s c o s   90 °   - F D C ⋅ D E _ D B _ - F D E ⋅ c o s ⁡ ( 0 ° ) = 0

0 - F D C ⋅ 4 4 2 + 2 2 - F D E = 0

Então encontramos:

F D E = - 1200   N = - 1,2   k N

Que nesse caso, por fazer uma força de reação nesse sentido, está sob tração.

Passo 3

Agora, vamos para a junta E , pois a C , nós já descobrimos as forças que atuam nela.

No eixo x :

∑ F x = 0

900 - F E C - F E B ⋅ A B _ E B _ - F D E + F E A ⋅ c o s ⁡ ( 90 ° ) = 0

900 - 0 - F E B ⋅ 2 2 2 + 2 2 - 0 = 0

Assim encontramos:

F E B = 1272,8   N ≈ 1,27   k N

Estando ela em compressão.

Agora no eixo y :

∑ F y = 0

900 ⋅ c o s c o s   90 °   + F E B ⋅ E A _ E B _ - F D E + F E A = 0

0 + 1272,8 ⋅ 2 2 2 + 2 2 + 1200 + F E A = 0

Então encontramos:

F E A = 2100   N ≈ - 2,1   k N

Que nesse caso, por fazer uma força de reação nesse sentido, está sob tração.

Resposta

F E C = 0 k N

F D C = F C B = 1,34   k N (Compressão)

F D E = 1,2   k N (Tração)

F E B = 1,27   k N (Compressão)

F E A = 2,1   k N (Tração)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6.49. Uma treliça de telhado de uma água é carregada tal como mostra a figura. Determine a força nos elementos CF, DE e DF.
6.50. Uma treliça de telhado de uma água é carregada tal como mostra a figura. Determine a força nos elementos EG, GH e HJ.
6.53. Uma treliça de telhado Pratt é carregada tal como mostra a figura. Determine a força nos elementos CE, DE e DF.
6.54. Uma treliça de telhado Pratt é carregada tal como mostra a figura. Determine a força nos elementos FH, FI e GI.
Determine a força em cada elemento da treliça mostrada na figura.