Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 49

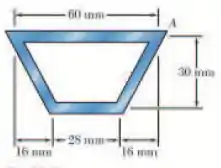
Uma viga extrudada tem a seção transversal mostrada na figura é uma parede de espessura uniforme de 3 ymm. Para força cortante vertical de 10 kN, determine (a) o tensão de cisalhamento no ponto A, (b) a tensão de cisalhamento máxima na viga. Além disso, esboce o fluxo de cisalhamento na seção transversal.

Passo 1

Muito bem turminha, vamos começar com os nosso cálculos:

t a n   α = 16 30 α = 28,07 °

Lado:

A = 3   s e c   α 30 = 102   m m 2

I _ = 1 12 3   s e c   α 30 3 = 7,6498 × 10 3   m m 4

Y 0 _ = Σ A y _ Σ A = 8,46 × 10 3 468 = 18,077   m m

I = Σ A d 2 + Σ I _ = 70,31 × 10 - 6   m m 4   = 70,31 × 10 - 9   m 4

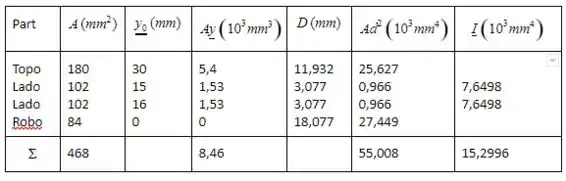
Agora, vamos calcular o (a):

Q A = 180 11,932 = 2,14776 × 10 3 m m 3 = 2,14776 × 10 - 6 m 3

t = 2 3 × 10 - 3 = 6 × 10 - 3 m

τ A = V Q I t = ( 10 × 10 3   ) ( 2,14776 × 10 - 6   ) ( 70,31 × 10 - 9 ) ( 6 × 10 - 6   ) = 50,9 × 10 6   P a

τ A = 50,9   M P a

Agora, vamos calcular o (b):

Q m = Q A + ( 2 ) ( 3   s e c   ) ( 11,932 ) 1 2 × 11,932

= 2,14776 × 10 3 + 484,06 = 2,6318 × 10 3   m m 3

= 2,6318 × 10 - 3   m 3 t = 6 × 10 - 3   m

τ m = V Q m I t = ( 10 × 10 3   ) ( 2,6318 × 10 - 6 ) ( 70,31 × 10 - 9 ) ( 6 × 10 - 3 ) = 62,4 × 10 6   P a τ m = 62,4   M P a

Q b = ( 28 ) ( 3 ) ( 18,077 ) = 1,51847 × 10 3   m m 3

τ B = Q B Q A τ A = 1,51847 × 10 3 2,14776 × 10 3 50,9 = 36,0   M P a

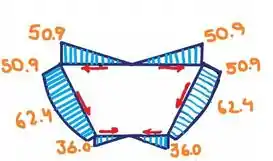
Resposta

Então gurizada, conseguimos encontrar nossas respostas, que são em (a) τ A = 50,9   M P a e em (b) τ m = 62,4   M P a . e para o fluxo temos τ B = 36,0   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma coluna é fabricada conectando os perfis de aço laminado mostrados na figura porparafusos de diâmetro 3/4 pol. espaçado longitudinalmente a cada 5 pol. Determine a tensão de cisalhamento média nos
Uma viga consiste em três pranchas conectadas por parafusos de aço espaçados longitudinalmente de 225 mm conforme mostrado. Sabendo que a força cortante na viga é vertical e igual a 6 KN e que a tensã
Duas placas de aço de 12 x 220 mm de seção transversal retangular são soldadas a um perfil W250 x 58 como mostra a figura. Determine a maior força cortante vertical admissivel para que a tensão de cis
Uma viga consiste em cinco pranchas com seção transversal de 1,5 x 6 in. Conectadas por parafusos de aço espaçados longitudinalmente de 9 in. Sabendo que a força cortante na viga é vertical e igual a
A seção transversal de uma viga extrudada é um quadrado vazado de lado a = 3i n . e espessura t = 0,25 . Para uma força cortante vertical de 15k i p s ,determine a tensão de cisalhamento máxima na vig