Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 6.Problemas - Ex. 55

Para uma viga feita de dois ou mais materiais diferentes módulos de elasticidade. Mostre que a Equação (6.6)

τ m e d = V Q I t

permanece válida desde que Q e I sejam calculados usando a seção transformada da viga (ver Seção 4.4). e que t seja a largura real da viga em que τ m e d é calculado.

Passo 1

Então gurizada, vamos começar? bora calcular! Considere nosso esboço a seguir :D

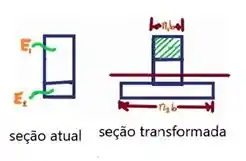
Seja E r e f um módulo de elasticidade de referência:

n 1 = E 1 E r e f n 2 = E 2 E r e f ETC

Passo 2

As larguras b da seção real são multiplicadas por n para obter a seção transformada. O estresse de flexão e distribuição na seção transversal é dada por:

σ x = - n M y I

onde I é o momento de inércia da seção transversal transformada em y é medido a partir do centro da seção transformada.

A força de cisalhamento horizontal ao longo do comprimento:

Δ H =   - ∫ Δ σ x d A = ∫ n ( Δ M ) y I d A = ( Δ M I ∫ n y d A = Q ( Δ M ) I

Passo 3

Q = ∫ n y d A = p r i m e i r o   m o m e n t o   d a   s e ç ã o   t r a n s f o r m a d a

fluxo do cisalhamento: q = Δ h Δ x = Δ M Δ x Q I = V Q I

“q” é distribuído pela largura real de “t”, portanto: τ = q t

τ = V Q I t

Resposta

τ = V Q I t .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Saber que um determinado cisalhamento vertical V causa uma tensão de cisalhamento máxima de 75 MPa em uma viga extrudada tendo a seção transversal mostrada, determine o tensão de cisalhamento nos três
Uma coluna é fabricada conectando-se os perfis de aço laminado mostrados na figura por parafusos de 19,05 mm de diâmetro espaçados longitudinalmente a cada 190,5 mm. Determine a tensão de cisalhamento
Três tábuas, cada uma com 50,8 mm de espessura, são pregadas entre si para formar uma viga que está submetida a uma força cortante vertical. Sabendo que a força cortante admissível em cada prego é de
Três tábuas são conectadas por parafusos com 3 8 in de diâmetro com espaçamento longitudinal de 6 in. ao longo do eixo longitudinal da viga. Para uma força cortante vertical na viga igual a 2,5 kips,
Para a viga e o carregamento mostrados, considere a seção n-n e determine (a) a maior tensão de cisalhamento naquela seção e (b) a tensão de cisalhamento ao ponto a.