Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 16
A viga é feita de um material cerâmico cuja tensão de flexão admissível é = 5 MPa e tensão de cisalhamento = 2,8 MPa. Determine a largura b da viga, se a altura for h=2b.
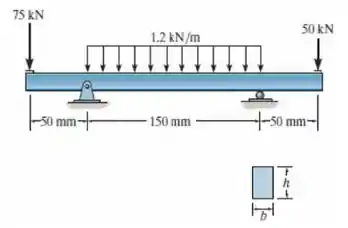
Passo 1
Antes de tudo, vamos fazer o Diagrama de Corpo Livre da nossa viga:
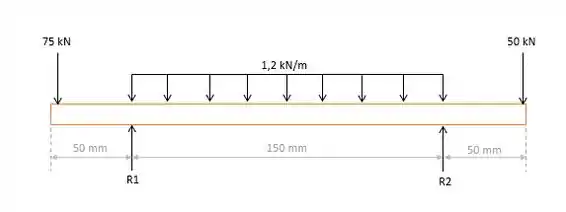
Pelo equilíbrio estático, temos que o somatório de forças e o somatório dos momentos são iguais a zero:
Agora, com os valores de todas as forças em mãos, podemos visualizar os esforços na viga.
Assim, podemos ver que e .
Passo 2
Então, precisamos dar uma olhada na seção transversal:
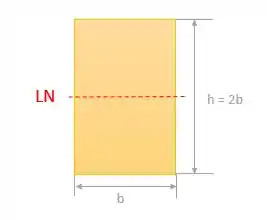
O Momento de Inércia I é de um retângulo é dado por:
A maior distância c até a linha neutra é igual a , assim, podemos calcular:
O enunciado nos diz que, , então:
Portanto, o tamanho máximo da nossa espessura b para que não ultrapassar a tensão de flexão admissível é de 104mm. Entretanto, é preciso conferir se a viga não irá cisalhar.
A força cortante máxima continua a mesma, assim como o momento de inércia; t é a largura da seção transversal, portanto t=b. Dessa forma, precisamos calcular apenas o Q.
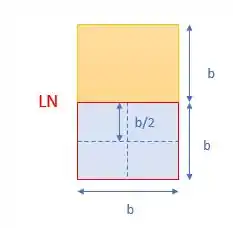
Q é calculado como a multiplicação da área em azul (maior área até a linha neutra) pela distância do centroide dessa área até a linha neutra. Ou seja:
Voltando para o cálculo da tensão de cisalhamento:
Ou seja, a tensão gerada irá cisalhar a viga antes que ela atinja sua tensão de flexão máxima admissível. Resultado: essa condição é FALSA.
Passo 3
Para garantir que a viga não cisalhe, devemos calcular a partir a espessura b a partir da sua tensão máxima de cisalhamento. Voltando para a fórmula anterior: