Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 47
Determine a força no elemento da treliça carregada.
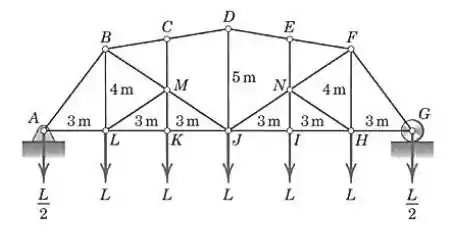
Passo 1
A carga total (vindo de cima) que a treliça precisa suportar terá que ser dividia igualmente nos apoios e , então:
Passo 2
Agora vamos aplicar o método das seções para encontrar a força em .
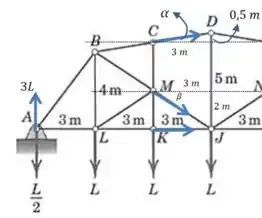
E estamos considerado uma seção que acaba na linha dos pontos e . Os ângulos e desenhados podem ser calculados da seguinte forma:
E então vamos aplicar a condição de equilíbrio das forças na direção vertical:
E então:
E agora precisamos encontrar a força para poder resolver essa expressão.
Passo 3
Ainda olhando para a mesma seção que desenhamos no passo anterior, vamos calcular o momento em relação ao ponto , pois nesse caso e terão momento nulo.
E o sinal negativo indica que é uma força de compressão. Substituindo isso na nossa equação anterior:
E essa é uma força de tração, em acordo com o desenho que fizemos.
Resposta
A força é (tração).