Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 44
44. Determine a força nos membros e da treliça e indique se os membros estão sob tração ou compressão.
Passo 1
Para começar a resolver o problema, primeiro vamos analisar o digrama de corpo livre a seguir:
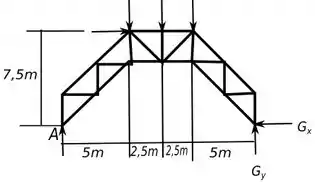
Observando o digrama, vemos que será necessário determinar e , já que eles influenciam os membros que queremos determinar e vamos fazer isso através das equações de equilíbrio do momento no ponto , pois assim não contribui para essa conta, e as equações de equilíbrio da força.
Tendo isso vamos fazer um corte que passa pelos membros e , para nos facilitar a análise e assim descobrir o valor das forças através das equações de equilíbrio.
Inicialmente vamos considerar todas as forças como sendo de tração, caso alguma apareça de forma negativa, saberemos que ela não é de tração, mas sim de compressão.
Passo 2
Agora vamos determinar :
Vamos determinar :
Passo 3
Agora vamos analisar o digrama de corpo livre da seção que sofreu o corte mencionado no passo 1.
Agora vamos aplicar as equações de equilíbrio.
Vamos começar com o ponto , já que e não contribuem para o momento em .
Então:
Como o resultado foi negativo, essa força não é uma força de tração, mas sim de compressão.
Passo 4
Agora vamos analisar o ponto para encontrarmos .
Como o resultado foi positivo, essa força é realmente uma força de tração.
Passo 5
Para achar , basta usar a equação de equilíbrio da força na direção , que é a seguinte:
Então é só somar as forças nessa direção e igualar a zero, com isso acharemos
Então:
Passo 6
Agora para achar a última força , basta usar o método dos nós no ponto . Vamos analisar só a equação do equilíbrio referente a .
Como o resultado foi positivo, essa força é realmente uma força de tração.