Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 30

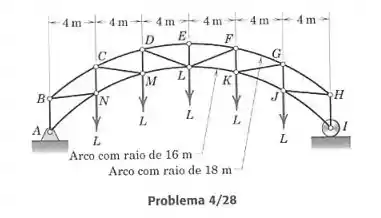
Determine a força no elemento da treliça carregada.

Passo 1

Vamos calcular as forças pelo método dos nós, aplicando as equações de equilíbrio no eixo e no eixo para cada nó, começando por , depois indo para , e finalmente . Primeiro vamos achar a reação feita pelo pino em . Depois, pra fazer as equações pra cada pino precisamos das coordenadas de cada ponto, para termos os ângulos que os elementos fazem com a horizontal.

Passo 2

Primeiro, como o apoio em não faz força horizontal também não. Isso significa que a força no elemento é nula, pois não há outra força capaz de equilibrar uma carga horizontal em . Agora, pela simetria da treliça e aplicando o equilíbrio de forças vertical, temos:

Consequentemente, a força no elemento é de compressão e:

Passo 3

Vamos encontrar as coordenadas dos pontos. Sendo a origem o centro dos arcos, para os pontos do arco de cima temos um raio de 18m, então:

As coordenadas do ponto que está no meio são . Agora vamos achar para os pontos , e .

Para os pontos e que estão no arco de baixo de 16 m de raio:

Passo 4

Vamos agora fazer as equações de equilíbrio para o nó B:

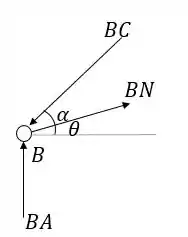
Encontramos os ângulos através das coordenadas dos pontos:

Para o equilíbrio das forças horizontais:

Agora verticais:

Substituindo pelo valor de encontrado no Passo 2:

Agora substituimos por :

Agora voltando para a equação anterior encontramos :

Passo 5

Agora vamos para o nó N:

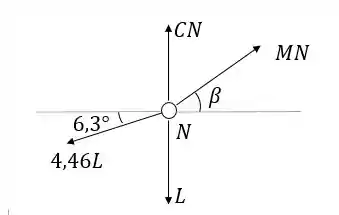
Pra achar , fazemos o mesmo procedimento:

Então fazemos a equação de equilíbrio das forças horizontais:

Agora em :

Substituindo o valor de e os senos:

Como o valor deu negativo, quer dizer que a força é de compressão e ntão de tração:

Passo 6

Agora vamos ao nó C:

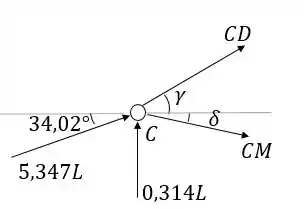
Novamente, primeiro achamos os ângulos:

Agora vamos às equações:

Isolamos pra substituir na próxima equação:

Agora para as forças verticais:

Substituindo os senos e o valor de encontrado anteriormente:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a estrutura e carregamento mostrados na figura, determine os componentes de todas as forças atuando no elemento A B C .

Um binário M de intensidade 1,5 k N ⋅ m é aplicado na manivela do sistema de motor mostrado na figura. Para cada uma das duas posições mostradas, determine a força P necessária para manter o sistema e

Usando o método dos nós, determine a força em cada elemento da treliça mostrada na figura. Indique se cada elemento está sob tração ou compressão.

Usando o método dos nós, determine a força em cada elemento da treliça de passo duplo mostrada na figura. Indique se cada elemento está sob tração ou sob compressão.

38. A treliça mostrada na figura consiste em nove elementos e é sustentada por uma rótula em A , por duas pequenas hastes de conexão em B e uma pequena haste de conexão em C . Determine a força em cad