Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 2.Problemas - Ex. 116
A porta de acesso é mantida na posição aberta a por uma corrente . Se a força trativa na corrente é de , determine a projeção desta força sobre o eixo diagonal da porta.
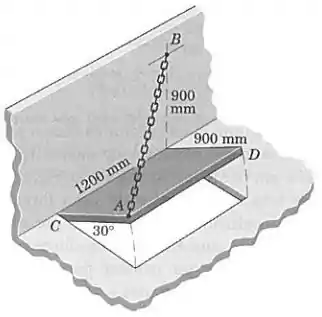
Passo 1
De acordo com a representação dos eixos , e na figura a seguir, as coordenadas em metros do ponto são ou , e as do ponto são :
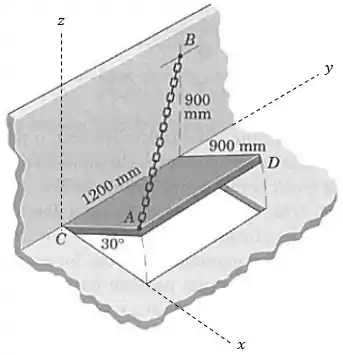
Logo, o comprimento será:
Assim, para o vetor da força trativa na corrente, temos:
E então:
Passo 2
Além disso, o comprimento será:
Assim, para o vetor unitário ao longo de , temos:
E então:
Passo 3
Por fim, podemos determinar a projeção da força sobre o eixo diagonal por meio do produto escalar:
Resposta
Exercícios de Livros Relacionados
Determine a intensidade da componente projetada da força F = 300N que atua ao longo da linha O A .
Determine o ângulo θ entre os cabos A B e A C .
Se F possui uma intensidade de 250N , determine a intensidade de suas componentes projetadas que atuam ao longo do eixo x e do cabo A C .
Determine os componentes x , y e z da força F que atua no tetraedro como mostrado. Os valores de a , b e c e F são conhecidos e M é o ponto médio da aresta A B .
145- Um role de uma trena com 30m de comprimento tem uma massa de 0.283k g . Calcule a deflexão h na metade da fita quando ela é esticada entre dois pontos, situados no mesmo nível, por uma força trat