Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 50
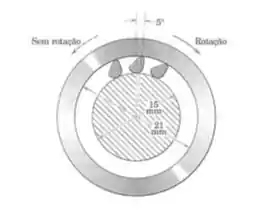
6/50) A embreagem de rotação em miniatura é projetada para permitir que o anel externo gire no sentido horário em relação ao eixo (hachurado) , mas impede rotação no sentido anti-horário . Isso é obtido pelo engaste por atrito das engrenagens (apenas três são mostradas ) . Calcule o coeficiente de atrito mínimo , , para as superfícies em contato , de forma a impedir rotação do anel externo no sentido anti-horário .
Passo 1
Então galera , organizando o que foi fornecido , temos que :
Nós sabemos que para , o deslizamento ocorreria primeiro em .
Além disso , utilizando a relação demonstrada nesta seção , sabemos que :
Passo 2
Bom pessoal , analisando o triângulo indicado na figura do enunciado , pela lei dos cossenos , temos que :
Sendo assim , isolando e substituindo os valores que jáconhecemos , obtemos que :
Da mesma , lei dos senos achamos que :
Portanto ,
Sendo assim ,
Resposta
Tranquilo pessoal? Então partiu resolver mais questões