Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 82
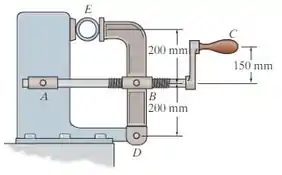
Determine a força horizontal exigida que deve ser aplicada perpendicularmente à manivela para desenvolver uma força de fixação de no cano. O parafuso de rosca quadrada simples tem um diâmetro médio de e um passo de . O coeficiente de atrito estático é . Nota: o parafuso é um elemento de duas forças, pois está contido dentro de colares em e , presos por pinos.
Passo 1
Um bom início de questão para mecânica é sempre que possível (na maior parte das vezes vai ser) desenhar o diagrama de corpo livre do objeto em questão. Isso vai nos ajudar e muito a entender o que se passa na questão e o que queremos encontrar!
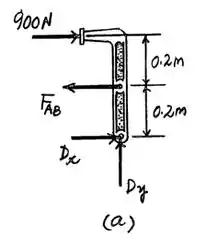
Passo 2
Precisamos encontrar o valor da força do parafuso. Um jeito de calcular ela é através do momento em relação ao ponto ! Em toda situação de equilíbrio, sabemos que o somatório dos momentos é igual a zero. Assumindo o sentido anti-horário como positivo, temos:
Passo 3
Galera, para um parafuso de rosca quadrada, o ângulo de passo é determinado a partir de . Aqui, é o passo da rosca e é o raio médio da rosca. Tendo essa ideia em mente, vamos calcular o ângulo de passo da nossa questão:
Passo 4
O ângulo de atrito estático para o parafuso de rosca quadrada é dado por . Logo,
Passo 5
Vamos dizer que . Assim, a equação para o momento do parafuso é dada por:
Substituindo os valores na equação, temos:
Resposta
A força horizontal é igual a: