Os três blocos de pedra têm pesos , e . Determine a menor força horizontal que deve ser aplicada ao bloco a fim de mover esse bloco. O coeficiente de atrito estático entre os bloco e entre o piso e cada bloco .
Passo 1
O problema pede que descubra a menor força horizontal para os blocos sairem do equibrio.
Bom galera, pra facilitar a gente começa fazendo um diagrama de corpo livre dos blocos como se fossem um só.
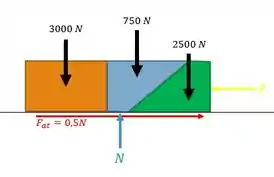
Passo 2
Beleza, a gente pode começar calculando a força Normal, que é a força de reação do solo, que anula a força peso total:
Então o atrito em vermelho, fica:
Então essa é a força que deve ser vencida para o sistema todo entrar em movimento, então:
Passo 3
Calma, esse pode não ser nosso resultado, caso um dos bloco deslize entre si, então vamos olhar bloco por bloco, começando por :
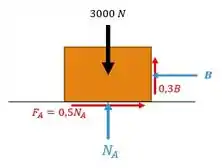
A gente pega as forças na vertical primeiro porque temos o peso, ai a gente analisa e encontra:
E na horizontal:
Substituindo na primeira equação a gente fica com:
E a gente descobre então que:
Com isso substituindo no que a gente já tem a gente encontrar:
Que é a força que precisa aplicar em para vencer o atrito.
E:
Passo 4
Agora o bloco :
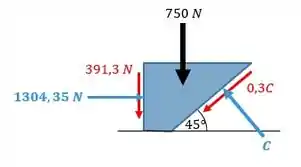
Denovo começando pela vertical:
Assim a gente encontra:
Então com isso:
E se fizermos o mesmo no bloco , encontramos:
Ou sejá é preciso que a força seja essa para que os blocos deslizem entre si, então o quando ultrapassar todos os blocos deslizaram juntos.