Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 3.Problemas - Ex. 26

3.26. Determine as trações desenvolvidas nos fios CD, CB e BA e o ângulo θ necessário para o equilíbrio do cilindro E de 15   k g e do cilindro F de 30   k g .

Passo 1

Fala! Queremos descobrir θ para que essa situação toda esteja em equilíbrio. E a força em cada cabo. O que quer dizer que as resultantes das forças em cada eixo devem zerar:

F R x = 0

F R y = 0

Primeira coisa é fazer o diagrama de corpo livre para C e B:

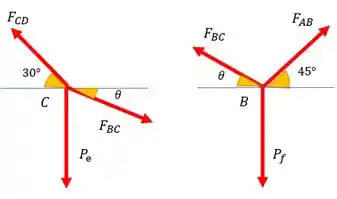
Para resolver esse exercício usaremos as equações de equilíbrio nos eixos x e y. A gente acha expressões para as componentes de F R e iguala ambas a zero. Primeiro faremos isso para o ponto C da figura. Depois disso faremos a mesma coisa para o ponto B na figura. Bora!

Passo 2

Vamos começar calculando F R x no ponto C.

F R x = F B C ⋅ cos ⁡ θ - F C D ⋅ cos ⁡ 30 ° = 0

Então

F B C ⋅ cos ⁡ θ = F C D ⋅ cos ⁡ 30 °

Agora vamos fazer o mesmo para F R y

F R y = - F B C ⋅ sin ⁡ θ + F C D ⋅ sin ⁡ 30 ° - 15 = 0

Aqui eu to usando k g f , (kilograma-força) pra unidade de força, beleza? Pra calcular essa força em newtons, é só multiplicar por g no final ;)

Isso é para a gente facilitar nossas continhas.

Passo 3

Agora vamos usar a equação de equilíbrio no ponto B

F R x = F B A ⋅ cos ⁡ 45 ° - F B C ⋅ cos ⁡ θ = 0

Então

F B A ⋅ cos ⁡ 45 ° = F B C ⋅ cos ⁡ θ

Agora vamos fazer o mesmo para F R y

F R y = F B A ⋅ sin ⁡ 45 ° + F B C ⋅ sin ⁡ θ - 30 = 0

Passo 4

Agora temos 4 equações e quatro incógnitas

F B C ⋅ cos ⁡ θ = F C D ⋅ cos ⁡ 30 °         ( 1 )

- F B C ⋅ sin ⁡ θ + F C D ⋅ sin ⁡ 30 ° = 15         ( 2 )

F B A ⋅ cos ⁡ 45 ° = F B C ⋅ cos ⁡ θ         ( 3 )

F B A ⋅ sin ⁡ 45 ° + F B C ⋅ sin ⁡ θ = 30         ( 4 )

Vamos começar substituindo (1) em (3)

F B A ⋅ cos ⁡ 45 ° = F C D ⋅ cos ⁡ 30 °

então

F B A = F C D ⋅ cos ⁡ 30 ° cos ⁡ 45 ° = 1,22 ⋅ F C D

Passo 5

Elevando (1) e (2) ao quadrado e somando temos

F B C 2 ⋅ cos 2 ⁡ θ + F B C 2 ⋅ sin 2 ⁡ θ = F C D 2 ⋅ cos ⁡ 30 ° 2 + F C D ⋅ sin ⁡ 30 ° - 15 2    

    F B C 2 = F C D 2 ⋅ cos ⁡ 30 ° 2 + F C D 2 ⋅ sin ⁡ 30 ° 2 + 15 2 - 2 ⋅ 15 ⋅ F C D ⋅ sin ⁡ 30 °

F B C 2 = F C D 2 + 15 2 - 2 ⋅ 15 ⋅ F C D ⋅ sin ⁡ 30 °

F B C 2 = F C D 2 - 15 ⋅ F C D + 225

Agora fazendo o mesmo em (3) e (4)

F B A 2 ⋅ cos ⁡ 45 ° 2 + 30 - F B A ⋅ sin ⁡ 45 ° 2 = F B C 2 ⋅ cos ⁡ θ 2 + F B C 2 ⋅ sin ⁡ θ 2

F B C 2 = F B A 2 ⋅ cos ⁡ 45 ° 2 + 30 2 + F B A 2 ⋅ sin ⁡ 45 ° 2 - 2 ⋅ 30 ⋅ F B A ⋅ sin ⁡ 45 °

F B C 2 = F B A 2 + 30 2 - 2 ⋅ 30 ⋅ F B A ⋅ sin ⁡ 45 °

F B C 2 = F B A 2 + 30 2 - 2 ⋅ 30 ⋅ F B A ⋅ sin ⁡ 45 °

F B C 2 = F B A 2 - 42,43 ⋅ F B A + 900

Passo 6

Então

F C D 2 - 15 ⋅ F C D + 225 = F B A 2 - 42,43 ⋅ F B A + 900

Logo

F C D 2 - 15 ⋅ F C D + 225 = 1,22 2 ⋅ F C D 2 - 42,43 ⋅ 1,22 ⋅ F C D + 900

- F C D 2 + 15 ⋅ F C D + 1,22 2 ⋅ F C D 2 - 42,43 ⋅ 1,22 ⋅ F C D - 225 + 900 = 0

0,49 ⋅ F C D 2 - 36,76 ⋅ F C D + 675 = 0

Daqui tiramos que

F C D ≈ 42,9   k g f

Então podemos dizer que

F B A = 1,22 ⋅ F C D = 1,22 ⋅ 42,9 = 52,34   k g f

E por fim

F B C = 42,9 2 - 15 ⋅ 42,9 + 225 = 37,7   k g f

Passo 7

Agora vou converter todas essas forças para Newton

F C D = 42,9 ⋅ 9,81   N = 420,85   N

F B A = 52,34 ⋅ 9,81   N = 513,45   N

F B C = 37,7 ⋅ 9,81   N = 369,84   N

Passo 8

Agora só falta determina θ , vamos usar

F B A ⋅ cos ⁡ 45 ° = F B C ⋅ cos ⁡ θ        

θ = c o s - 1 F B A F B C ⋅ cos ⁡ 45 ° = c o s - 1 52,34 37,7 ⋅ cos ⁡ 45 ° ≈ 11 °

Show!

Obs: Ficamos diferentes do gabarito, mas estamos certinhos 😉

Resposta

F C D = 42,9   k g f = 420,85   N

F B A = 52,34   k g f = 513,45   N

F B C = 37,7   k g f = 369,84   N

θ = 11 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desenhe o diagrama de corpo livre para os problemas a seguir. a) A lança no Problema 5.37. b) O anteparo no Problema 5.39. c) O elemento horizontal no Problema 5.41.
Quando no nível do terreno, o carro é colocado em quatro escalas individuais — uma em cada pneu. As leituras das escalas 4450N em cada roda dianteira e 2950N em cada pneu traseiro. Determine a coorden
A força de módulo P=180N é aplicada na manivela da máquina estacionária, como mostrada. Escreva as reações da força e do momento em O como vetores. Despreze o peso conjunto da manivela.
Uma ciclista aplica uma força de 40N na alavanca de freio de sua bicicleta, conforme mostrado. Determine a tensão correspondente T transmitida ao cabo do freio. Despreze o atrito no pivô O.
Determine a magnitude da força P necessária para levantar uma extremidade da caixa de 250k g com o carrinho da alavanca, conforme mostrado. Declare quaisquer suposições.