Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.10 - Ex. 214
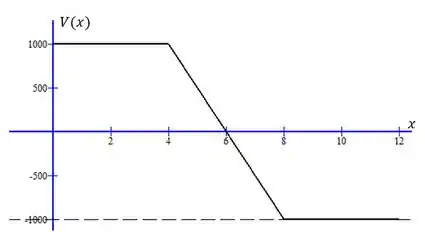
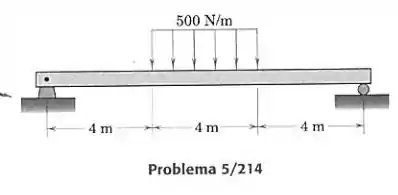
Construa os diagramas de cortante e de momento para a viga, que sustenta a carga uniforme de 500 N por metro de comprimento da viga, distribuída ao longo da seção média. Determine o momento fletor máximo e sua posição.
Passo 1
Vamos calcular a força cortante e o momento fletor para cada pondo de distância até da viga. Pra isso faremos um cortes em pontos de coordenada e resolveremos as condições equilíbrio para uma parte dela. Perceba que pela simetria, só precisamos calcular os valores para metade da viga, e definimos os valores para a outra metade espelhando a função em torno do meio ( fazendo trocar o sinal de e manter o sinal para (pela convenção do sentido de e ).
Passo 2
Primeiro devemos achar as forças externas atuando na viga. Calculamos a resultante da distribuição de forças na viga pela área da região do diagrama:
Pela simetria, cada apoio deverá fazer para cima uma força de 1000 N.
Passo 3
Agora, para o cálculo de e , iremos separar a viga em duas regiões, uma entre 0 e 4 m que não sofre a carga das forças distribuídas, e a outra entre 4 e 6 m. Para a primeira região, fazemos um corte e observamos em diagrama de corpo livre:
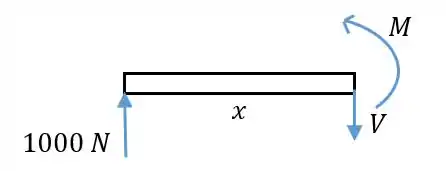
Pelo equilíbrio em , temos:
E para o equilíbrio dos momentos do ponto de coordenada :
Passo 4
Agora vamos olhar para a região . Agora já temos o efeito da distribuição das cargas em cima da viga:
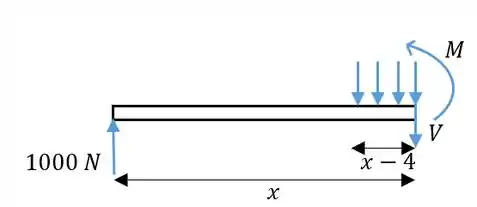
A resultande da parte da distribuição de carga é:
Então achamos pelo equilíbrio em :
Para achar o momento, vemos que a resultante das cargas aplicaas fica no meio da parte de tamanho . Então fazendo a soma dos momentos no ponto de coordenada :
Passo 5
Agora temos as expressões de e :
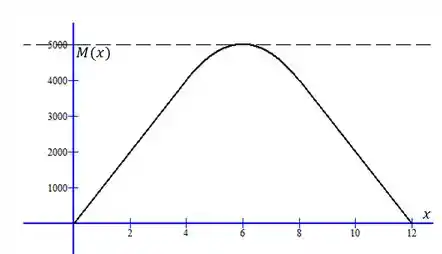
Esboçamos essas funções e espelhamos em torno de , trocando o sinal de :
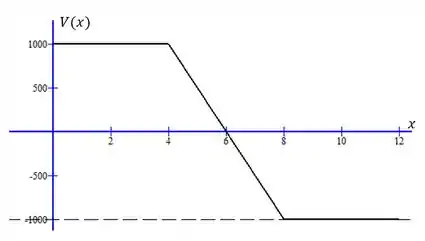
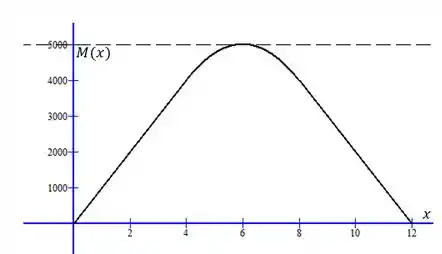
Fica claro pelo gráfico que o máximo de ocorre quando . Então:
Resposta
