Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 1
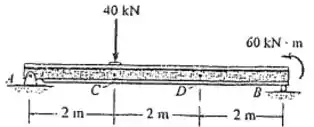
Determine a força normal e o esforço cortante internos, e o momento nos pontos e da viga. Assuma que o apoio em seja um rolete. O ponto está localizado logo à direita da carga de .
Passo 1
Fala, querido! Queremos os esforços internos em e . Para resolver esse tipo de questão tem um passo a passo. Só seguir que dá bom:
- Fazer DCL
- Achar reações de apoio
- seccionar o corpo nos pontos de referência e fazer a análise dessas seções, ou seja, fazer a análise das reações internas de cada membro seccionado.
E o que é legal é que essa análise é feita com as querinhas equações de equilíbrio. Bora lá!
Passo 2
Então, primeiramente, fazendo o DCL de todo o sistema é possível obter a reação exercida no ponto de apoio.
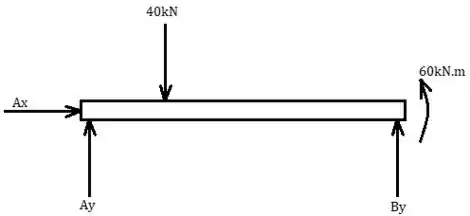
Como temos duas forças no ponto , vamos calcular o momento em relação a ele. Aí a gente nem precisa se preocupar com elas. Vamos considerar que o momento seja positivo no sentido anti-horário, então:
Também pode-se fazer o equilíbrio de forças para os dois eixos, tal que para o eixo :
E para o eixo :
Passo 3
Em seguida, pode-se fazer um “corte” nos pontos e e dividir a viga em partes que podem ser analisadas.
Vamos fazer um “corte” no ponto , olhar só para um dos lados da viga e posicionar as componentes das cargas internas nessa seção segundo a conveção de sentidos positivos para os esforços que foi adotado no livro.
Logo, fazendo o DCL da seção à esquerda do ponto e mostrando as forças e reações aplicadas, tem-se que:
Repara que a força de aparece porque nossa seção está a direita dela (como foi dito pelo enunciado).
Agora, fazendo o equilíbrio de forças em obtém-se:
Fazendo o equilíbrio de forças em :
O sinal negativo indica que o esforço cortante em atua para cima.
E aplicando o princípio dos momentos no ponto , considerando que o momento é positivo no sentido anti-horário, é possível ter:
Passo 4
Da mesma forma, fazendo o DCL da seção à direita de e mostrando as forças e reações aplicadas, tem-se que:
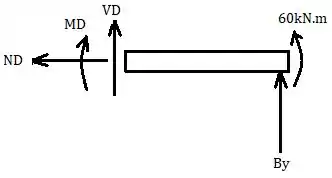
Agora, fazendo o equilíbrio de forças em obtém-se:
Fazendo o equilíbrio de forças em :
O sinal negativo indica que o esforço cortante em atua para baixo.
E aplicando o princípio dos momentos no ponto , considerando que o momento é positivo no sentido anti-horário, é possível ter:
Resposta