Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 24
Determine as forças normal e cortante e o momento fletor nos pontos e na viga composta de dois elementos. O ponto está localizado logo à esquerda da força de e do momento de binário de .
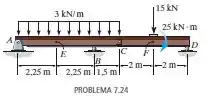
Passo 1
Eaiii... belezinha??
Nessa questão vamos usar as equações de equilíbrio estático:
- Somatório das forças em :
- das forças em :
- e do momento:
Ahhh... como temos uma viga composta, então vamos dividir em duas partes (que nos ajude a calcular o que queremos, né?)
Passo 2
Para o segmento :
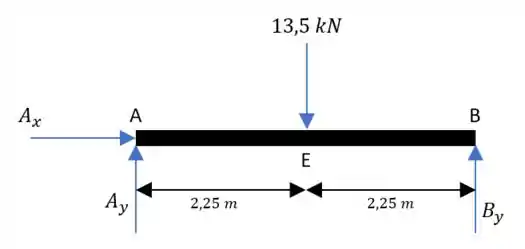
Lembrando que podemos trocar essa carga distribuída por uma equivalente concentrada, ok?
Fazendo o somatório das forças em :
Em :
E para o momento:
E daí:
Passo 3
Fazendo o corte em :
Fazendo o somatório das forças em :
Em :
E para o momento:
Passo 4
Agora vamos usar o segmento :
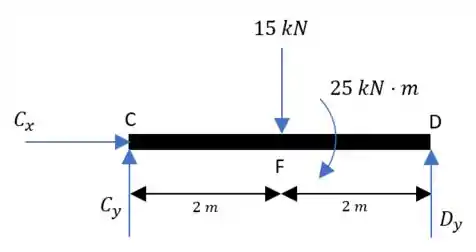
Fazendo o somatório das forças em :
Em :
E para o momento:
Daí:
Passo 5
Fazendo o corte em :
Fazendo o somatório das forças em :
Em :
E para o momento:
Ufaaaa... essa foi grande, heim!? Mas desanima não. Bora pra próxima.