Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 22
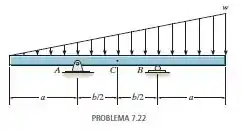
Determine a razão para a qual a força cortante será zero no ponto intermediário da viga.
Passo 1
Falaiii... beleza?
Nessa questão vamos precisar dos conceitos de estática:
- Somatório das forças em :
- em :
- e para o momento:
Já vamos mandar também o diagrama de corpo livre:
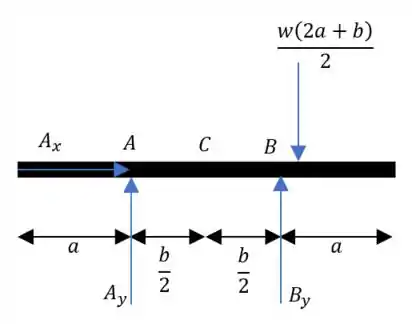
Lembrando que essa carga distribuída podemos substituir por uma pontual equivalente:
Passo 2
Fazendo o somatório das forças em :
Em :
E para o momento:
Passo 3
Fazendo o corte em :
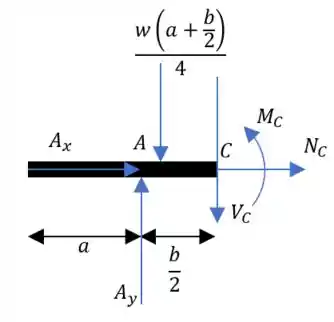
Lembrando de calcular a nova carga equivalente à carga distribuída:
Fazendo o somatório das forças em :
Como então:
Ufaa... foi mais uma... Que tal ir pra próxima??
Resposta
Exercícios de Livros Relacionados
O cabo suporta a carga distribuída uniforme de w 0 = 12k N / m . Determine a tração no cabo em cada apoio A e B .
Se o tubo tem uma massa por unidade de comprimento de 1500 kg/m, determine a tração máxima desenvolvida no cabo.
Se o tubo tem uma massa por unidade de comprimento de 1500 kg/m, determine a tração mínima desenvolvida no cabo.
Determine a tração máxima desenvolvida no cabo se ele estiver sujeito a uma carga uniforme de 600N / m .
Se a inclinação do cabo no apoio A é zero, determine a curva de deflexão y = f x do cabo e a tração máxima desenvolvida nele.