Esboce os diagramas de cortante e de momento para cada uma das quatro vigas carregadas e apoiadas como mostrado.

Passo 1
- A primeira viga pode ser dividida em 3 regiões de comprimento : antes da primeira força aplicada, entre as duas forças e depois da segunda força. Pela simetria, sabemos que as forças causadas pelos apoios são ambas iguais a . Vamos fazer diagramas de corpo livre para cada região:
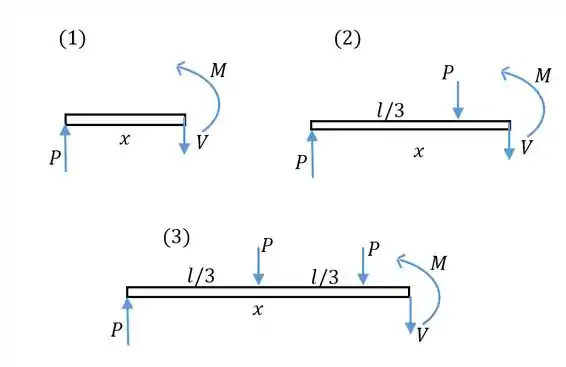
Aplicando o somatório das forças verticais e o momento no ponto de coordenada , achamos e . Na primeira região, temos:
Na segunda:
Na terceira:
Com isso, esboçamos os diagramas de e . é constante e igual a , depois é constante e igual a zero e depois constante e igual a . Representamos o gráfico de por :
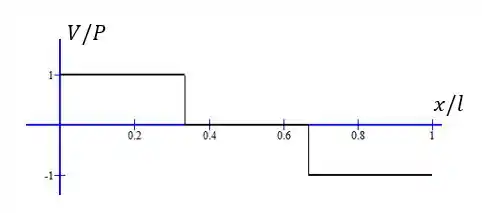
cresce linearmente na primeira região, depois é constante e igual a , depois decresce novamente até zero. Representamos o gáfico de em função de :
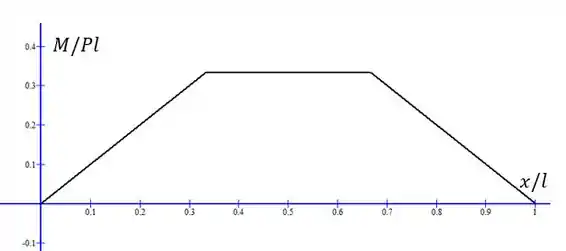
Resposta

