Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 17
Determine a razão de para a qual o esforço cortante será zero no ponto intermediário da viga com dupla extremidade em balanço.
Passo 1
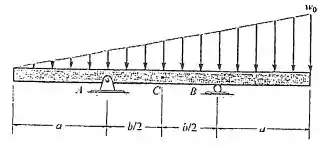
Para determinar o que se pede, deve-se fazer o diagrama de corpo livre da viga para que seja possível determinar alguma reação externa ao apoio da viga. Após isso, deve-se seccionar o corpo nos pontos de referência e fazer a análise dessas seções, ou seja, fazer a análise das reações internas do sistema.
Passo 2
Deve-se fazer o DCL da viga a fim de determinar alguma reação agindo nela. Então, tem-se:
Visto que há uma carga distribuída triangular na viga, ela gera uma força resultante dada por:
E a posição do seu centroide é dada por:
Então, supondo o sentido anti-horário como positivo e aplicando o princípio dos momentos em relação ao ponto B:
E fazendo o equilíbrio de forças no eixo :
Passo 3
Pelo fato de o ponto ser o ponto de interesse deve-se fazer um “corte” neste ponto da viga que terá uma de suas seções analisadas.
Logo, fazendo o DCL da seção à esquerda de e mostrando as forças e reações aplicadas, tem-se que:
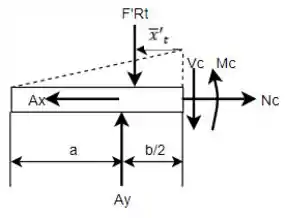
Como o comprimento da seção diminuiu, o valor da força resultante gerada pela carga distribuída é alterado. No entanto, como o ponto de análise é intermediário e a carga é linear, ela será metade do valor da extremidade, ou seja:
Por isso, a nova resultante terá o valor de:
Passo 4
Agora, com todas essas informações para verificar a condição do esforço cortante ser nulo é necessário fazer o equilíbrio de forças no eixo vertical, tal que:
Passando o segundo termo para o lado direito da equação:
Os termos semelhantes podem ser simplificados para obter:
E, por fim, isolando o termo :