Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas Fundamentais - Ex. 37
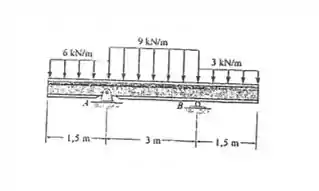
Determine a força resultante e especifique onde ela atua na viga, medindo a partir do ponto .
Passo 1
Queremos determinar a força resultante e indicar o local onde ela atua na viga medindo-se a partir do ponto mostrado na figura. Primeiramente devemos lembrar que podemos concentrar essas cargas distribuídas em um ponto, mas que ponto seria esse? Como as cargas distribuídas tem formato retangular o ponto onde podemos concentrá-las é na metade da distância desse carregamento, assim, nós teremos
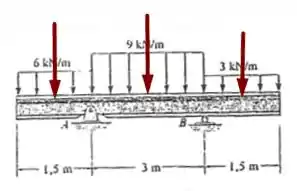
Ok, sabemos agora que elas podem ser concentradas ali, mas qual o sei valor? Para isso, basta multiplicarmos o valor da carga distribuída pela distância que ela abrange, ou seja, façamos a seguinte conta
Dessa forma, nossa distribuição de cargas fica sendo
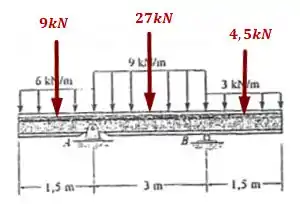
Passo 2
Feito isso, agora podemos calcular as componentes das forças resultantes na direção .
O sinal negativo indica que a força está apontando para baixo. A magnitude da força resultante será, então,
Até aqui temos a intensidade da força, mas resta-nos calcular onde essa força está agindo.
Para isso vamos utilizar a equação do momento gerado pela nossa força resultante, em relação ao ponto A:
Considerando o sentido anti-horário como positivo, esse momento será negativo, pois está no sentido horário...
Agora, vem cá comigo...
Concorda que o momento gerado pela força resultante, precisa ser igual ao momento gerado pelas 3 forças que geram essa resultante... em outras palavras...
E, assim, conseguiremos encontrar a posição em relação ao ponto que nossa força está agindo. Sendo assim, adotando o sentido anti-horário como positivo, e colocando as distâncias das forças até o ponto A, teremos:
Pronto, está concluído nosso exercício temos a força e a distância na qual essa força atua em relação ao ponto como nos foi solicitado.