Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 9.Problemas fundamentais - Ex. 1

Determine o centróide ( overset(-)(x) , overset(-)(y) ) da area sombreada.

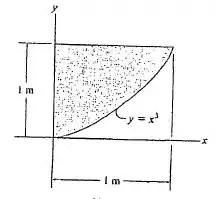
Passo 1

Falaaa! Queremos o centroide dessa região fofa.

O nosso primeiro passo aqui é calcular a área da região sombreada.

Passo 2

Um elemento diferencial retangular é considerado com uma espessura d y e cruza o limite em ( x , y ) .

A área do elemtno é expressada como d A = x d y

O centroide do elemtno de área está localizada a uma distância bar y = y do x eixo bar x = x // 2 do y eixo.

A área é limitada pela curva y = x^3

Reogarnixando os termos da equação acima.

x = y^(1 // 3)

Encontraremos a área do elemento diferencial.

d A = x d y

= y^(1 // 3) d y

Passo 3

Calcularemos o centroide bar x da área sombreada.

bar x = (int_A bar x d A)/(int_A d A)

Substituindo

bar x = (int_0^1 (1)/(2) ( y^(1 // 3) ) * ( y^(1 // 3) d y ))/(int_0^1 y^(1 // 3) d y)

bar x = ((1)/(2) int_0^1 ( y^(1 // 3) d y ))/(int_0^1 y^(1 // 3) d y)

Integrando os termos do numerador e denominador e aplique os limites.

bar x = ((1)/(2) |y^(((2)/(3) + 1)) // ((2)/(3) + 1)|_0^1)/(|y^(((1)/(3) + 1)) // ((1)/(3) + 1)|_0^1)

bar x = ((3)/(10) |y^(5 // 3)|_0^1)/((3)/(4) |y^(4 // 3)|_0^1)

bar x = ((3)/(10) [(1)^((5)/(3)) - (0)^((5)/(3))])/((3)/(4) [(1)^((4)/(3)) - (0)^((4)/(3))])

bar x = ((3)/(10) xx (4)/(3)) m

bar x = 0.4 m

Portanto, o centroide bar x da área sombreada é 0.4 m

Passo 4

Calcularemos o centroide bar y da área sombreada.

bar y = (int_A bar y d A)/(int_A d A)

Substituindo

bar y = (int_0^1 ( y ) * ( y^(1 // 3) d y ))/(int_0^1 y^(1 // 3) d y)

bar y = ((1)/(2) int_0^1 ( y^(4 // 3) d y ))/(int_0^1 y^(1 // 3) d y)

Integrando os termos do numerador e denominador e aplique os limites.

bar y = (|y^(((4)/(3) + 1)) // ((4)/(3) + 1)|_0^1)/(|y^(((1)/(3) + 1)) // ((1)/(3) + 1)|_0^1)

bar y = ((3)/(7) |y^(7 // 3)|_0^1)/((3)/(4) |y^(4 // 3)|_0^1)

bar y = ((3)/(7) [(1)^((7)/(3)) - (0)^((7)/(3))])/((3)/(4) [(1)^((4)/(3)) - (0)^((4)/(3))])

bar y = ((3)/(7) xx (4)/(3)) m

bar y = 0.5714 m

Portanto, o centroide bar y da área sombreada é 0.5714 m

Resposta

Portanto, o centroide bar x da área sombreada é 0.4 m

Portanto, o centroide bar y da área sombreada é 0.5714 m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a coordenada y do centroide do volume gerado pela revolução da área sombreada do triangulo direito em torno do eixo z por 90 ° como mostrado na figura.
Determine a coordenada y do centroide do volume gerado pela revolução da área sombreada do triangulo direito em torno do eixo z por 90 ° como mostrado na figura.
O carretel portátil é usado para enrolar e armazenar um ar Mangueira. A tensão na mangueira é de 100 N e uma vertical A força 200-N é aplicada à alça, a fim de estabilize a estrutura do carretel. Dete
Localize o centro de massa do corpo sólido homogêneo cujo volume é determinado girando a área sombreada em 360 ∘ em torno do eixo z.
Determine as coordenadas do centro de massa do corpo homogêneo.