Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 128
Determine a intensidade da força resultante que atua sobre a comporta em razão da pressão hidrostática. A comporta tem largura de 1,5 m e .
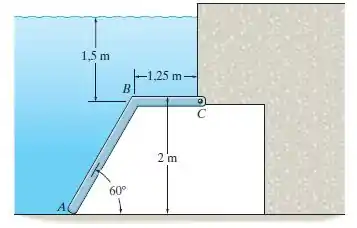
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos determinar a intensidade da força resultante sobre a comporta .
Para resolvermos esta questão nós precisamos dividi-la em duas partes: A parte horizontal e a parte inclinada .
Vamos determinar as forças sobre cada uma dessas partes e depois soma-las (vetorialmente viu!) para obter a força resultante!
Então, vamos as contas!
Passo 2
Vamos começar trabalhando com a parte horizontal . Por estar na posição horizontal, temos apenas a ação de uma força vertical, que é igual a:
A pressão nesta posição vezes a área da parte . Para calcularmos a pressão, temos:
E portanto, a força será:
Passo 3
Agora vamos para a barra . Como ela é inclinada (não está na horizontal, isso que importa), temos componentes horizontal e vertical.
Começando pela componente vertical, temos:
Sendo o volume de água acima da barra. Então, para este caso, temos:
Já a componente horizontal será:
Sendo e a intensidade da carga medida nos pontos e . Para obtermos os seus valores, basta multiplicar a espessura da comporta pela pressão em cada um dos pontos. Logo,
Então, a força horizontal será:
Passo 4
Para finalizarmos a questão temos que obter a força resultante. Mas, antes disso, vamos somar as forças (apenas as componentes na mesma direção)!!!
Logo, só somamos as forças na direção . Logo,
E como queremos a força resultante, temos:
E assim finalizamos a questão!