Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 127
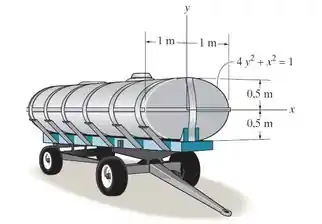
O tanque está cheio de um líquido com densidade de . Determine a força resultante que ele exerce sobre a placa elíptica no fundo, e a localização do centro de pressão, medido a partir do eixo .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Esta é uma questão bem direta ao ponto. Precisamos calcular a força resultante e a coordenada do ponto de aplicação desta força. Só isto mesmo.
O problema está exatamente na nossa geometria. Por ser uma elipse, vai dar um trabalhinho na hora de calcular. Mas também não é nada que a gente não consiga!
Relembrando, para calcularmos esses dois valores, temos que utilizar a seguinte relação:
Então, vamos as contas!
Passo 2
Vamos começar a questão calculando a força resultante. Para isto, vamos identificar quem é a função e os limites de integração da área.
A pressão nós sabemos que varia apenas com a altura da coluna de fluido. Como o sistema de coordenadas está no meio da placa, então, a pressão será escrita por:
A relação surge exatamente para corrigir a altura da coluna de fluido! Percebam que quando (topo da placa), a pressão é nula, já que não tem nenhuma coluna de fluido!
Já para os limites de integração, temos que lembrar um pouco de Cálculo! Analisando a nossa região como do tipo II, com limites e , temos:
Resolvendo esta integral nós obtemos:
Passo 3
Agora a gente tem que fazer algo semelhante ao Passo 2, só que para a equação de . O bom aqui é que boa parte desta relação já foi trabalhada (identificar a pressão e os limites de integração).
Então, o nosso trabalho será braçal. Apenas fazer contas!
Sendo assim, temos:
E assim finalizamos a questão!