Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 9.Problemas - Ex. 125
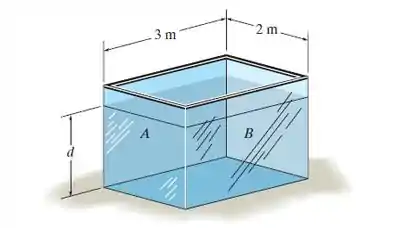
O tanque está cheio de água até uma profundidade . Determine a força resultante que a água exerce sobre a lateral e a lateral do tanque. Se for colocado óleo, em vez de água no tanque, até que profundidade ele deverá ser alcançar de modo que crie as mesmas forças resultantes? e .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Temos que ir com bastante calma nessa questão para não nos confundirmos. Aqui a gente tem dois casos.
No primeiro, o tanque está preenchido com água até uma altura . Com isto, devemos encontrar a força resultante que atua na lateral e .
Depois, só depois, trocamos a água pelo óleo. Com isto, devemos descobrir a altura que faz uma força resultante igual ao que calculamos anteriormente.
Então, vamos começar calculando os casos para o tanque com água!
Passo 2
Precisamos determinar a força horizontal nas laterais e do tanque. Elas serão dadas por:
Sendo e a intensidade da carga medida nos pontos superior e inferior do nível de água. Para obtermos os seus valores, basta multiplicar a largura da parede pela pressão em cada um dos pontos.
Começando pela parede , temos:
Então, a força horizontal será:
Agora temos que repetir o procedimento para a lateral . Portanto,
Então, a força horizontal será:
E assim a gente finaliza a primeira parte da questão!
Passo 3
Agora temos que descobrir a altura de óleo que fornece a força resultante nas paredes e .
E o procedimento é exatamente o mesmo! E para facilitar, basta olhar apenas uma das paredes! Escolhendo a parede , temos:
Então, a força resultante será:
Mas a força é exatamente ! Então, a altura de óleo será:
E assim finalizamos a questão!
Resposta
Para o tanque contendo água, temos:
Já a altura de óleo é .