Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 6.Problemas - Ex. 105
Determine as componentes horizontal e vertical da reação que os pinos em exercem sobre a estrutura. O cilindro possui uma massa de .
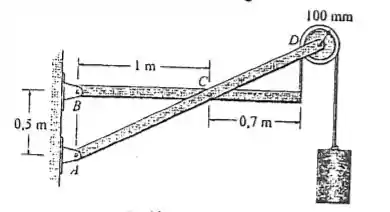
Passo 1
Dado que a questão foi bem direta ao ponto em relação ao que deseja, cabe a nós planejar como iremos resolvê-la. Primeiramente vamos traçar o diagrama de forças que servirão de base para encontrarmos as forças que precisamos no problema
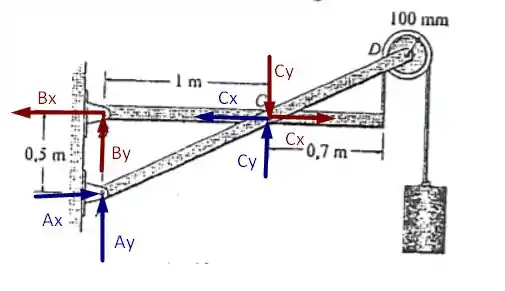
Passo 2
Utilizando as equações de equilíbrio para a região da estrutura que contém as forças em vermelho teremos
Passo 3
Agora, se observamos a parte da estrutura que contem as forças de azul teremos
Substituindo esse valor na equação vamos encontrar
Resposta
Exercícios de Livros Relacionados
O dispositivo mostrado é útil para suspender e posicionar painéis antes de prendê-los aos tirantes na parede. Estime o módulo P da força necessária para erguer o painel de 25k g . Explicite quaisquer
Uma placa de sinalização de uma auto-estrada, medindo 4m por 2m , é sustentada por um único poste, como mostrado. A placa, estrutura de suporte e o poste, juntos, tem uma massa de 300k g , tendo centr
Uma fita magnética, sob uma força trativa de 10N em D , passa, a velocidade constante, pelas polias guia e pela cabeça apagadora em C . Como resultado de um pequeno atrito nos mancais das polias, a fi
O vento soprando na direção normal ao plano da placa de sinalização retangular exerce uma pressão uniforme de 175N / m 2 , como indicado na figura. Determine as variações nas forças exercidas em A e B
Determine e plote, para qualquer ângulo θ entre pouco acima de zero e 45 ° , a razão T / m g entre as forças trativas necessária para manter em equilíbrio a barra esbelta. A barra A B de massa m é uni