Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 59
Determine as forças nos membros AB, AC e AD.
Passo 1
Primeiro, podemos ver que os pontos A, BC e D têm estas coordenadas:
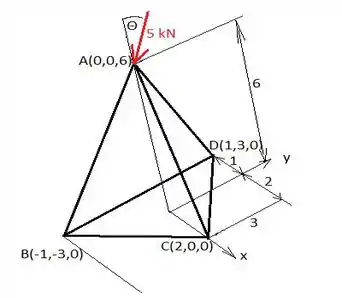
(A partir de agora todas as forças são dadas em quilo-Newtons e todas as distâncias são em metros)
Podemos supor que todas as forças são tensões e se obtivermos sinal negativo, isso significa apenas que é compressão.
Conhecendo as coordenadas de nossos pontos (seus vetores de raio), podemos encontrar vetores de deslocamento dos pontos B, C e D a A. Então, podemos dividir esses vetores com seus respectivos comprimentos para obter vetores unitários. Finalmente, as forças agindo sobre os membros serão seu vetor unitário multiplicado por suas magnitudes.
A equação para o vetor unitário é:
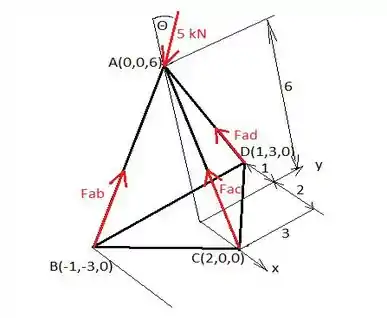
Passo 2
No nosso caso, o ponto A é sempre o ponto 1 e o ponto 2 são B, C e D.
Podemos simplesmente colocar nossas coordenadas nesta equação e obteremos:
E podemos multiplicar esses vetores unitários pela magnitude da força para obter a forma vetorial de nossas forças:
Força externa (E) é
Passo 3
Uma vez que a junta A está em equilíbrio sabemos que
Da primeira equação temos
Passo 4
Substituindo essa última e resolvendo em FAB temos
Se colocarmos na segunda equação, temos
E temos
Finalmente
Temos