Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 73
Determine a magnitude da reação do pino em ignorando o fato de que é um membro de duas forças e reconhecendo o fato de que é um membro de duas forças.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar o módulo da reação de apoio do pino em , devido ao peso no ponto , para duas situações: desconsiderando que é uma barra de duas forças e considerando que é uma barra de duas forças.
Show, então bora lá! Antes de resolver, vamos fazer o diagrama de corpo livre da situação para entendermos melhor o problema.
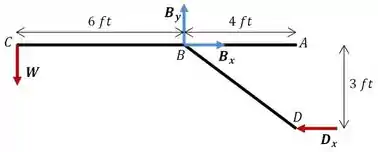
Primeiro vamos olhar para a treliça inteira, sem as reações em , como ela deve estar equilíbrio, podemos usar o somatório de momentos em torno de para descobrirmos a reação em .
Observe que nós escolhemos calcular o momento em torno do apoio porque isso elimina a necessidade de calcular as reações neste ponto, que não são nosso foco aqui.
Passo 2
Tranquilinho né? Agora vamos considerar a barra separadamente para calcular a componente vertical da reação em .
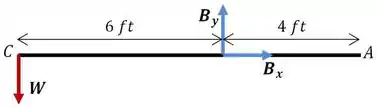
Novamente, como a barra deve estar em equilíbrio, vamos usar o momento em torno do ponto :
Passo 3
E, finalmente, olhando a barra , temos:
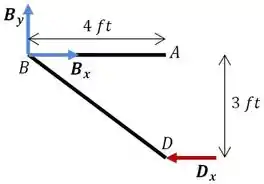
Agora vamos utilizar a equação de equilíbrio de forças na direção para determinar a componente horizontal da reação em :
Logo, o módulo da reação em é:
Passo 4
Tá quase acabando hein?! Não desiste não!! Hahaha
No caso precisamos considerar que é um elemento de duas forças:
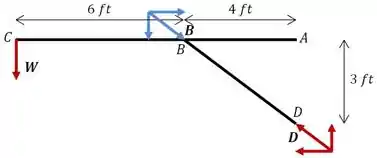
A componente horizontal da reação em vai ser a mesma do caso anterior, já que analisando a treliça inteira, dada pelo momento em torno de não se altera:
Mas, neste caso, o apoio em possui componentes vertical e horizontal. Portanto, podemos obter a componente vertical a partir da inclinação da barra , já que a força deve ser paralela a ela.
Passo 5
Com isso, o módulo da reação em é:
Como é um elemento de duas forças, as forças em e em devem ser iguais, logo:
Ufa! Essa já foi hein? Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 