Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 30

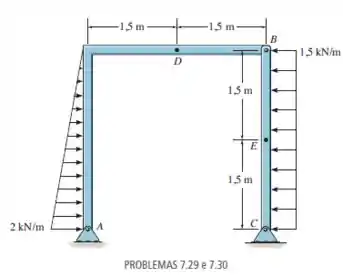
Determine as forças normal e cortante e o momento fletor no ponto E .

Passo 1

Oi tudo bem? Vamos resolver este exercício.

Queremos as forças normal e cortante e o momento fletor no ponto E .

Analisando a imagem do enunciado, podemos notar um pino em B este pino confere uma reação B x e B y no ponto.

O pino nos dá também uma saída para resolver problemas estaticamente indeterminados, uma vez que podemos analisar as barras ligadas pelo pino como elos independentes.

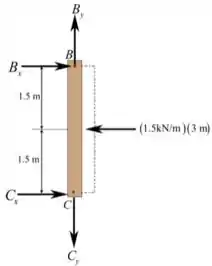
Considerando o momento em C , temos que:

∑ M C = 0

1,5 3 1,5 - B x ( 3 ) = 0

B x = 2,25   k N

Analisando o equilíbrio horizontal, temos que:

∑ F x = 0

B x + C x - 1,5 ( 3 ) = 0

C x + 2,25 - 4,5 = 0

C x = 2,25   k N

Vamos analisar o membro A B agora.

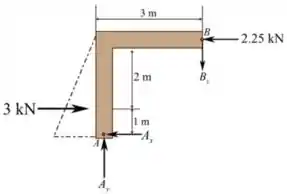
Considerando o momento em A , temos que:

∑ M A = 0

B x 3 - 1 2 2 3 1 - B y 3 = 0

3 B y = 2,25 3 - 3

B y = 1 , 25   k N

Passo 2

Agora que descobrimos as reações no ponto B , podemos cortar a seção B E e analisar as reações internas relacionadas ao ponto E .

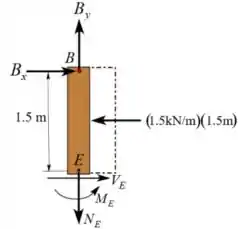
Vamos analisar o equilíbrio com relação à direção da normal:

∑ N = 0

- N E + B y = 0

N E = B y = 1 , 25   k N

Ou:

N E = 1 , 25   k N ↓

Agora analisando o equilíbrio com relação a cortante, temos que:

∑ V = 0

V E + B x - 1,5 ( 1,5 ) = 0

V E = 1,5 1,5 - 2,25

V E = 0

Analisando o equilíbrio com relação ao momento fletor, temos que:

∑ M = 0

M E = B x 1,5 - 1,5 1,5 0,75

M E = 2,25 1,5 - 1,5 1,5 0,75

Logo:

M E = 1 , 69   k N ⋅ m ↶

Resposta

N E = 1,25   k N ↓

V E = 0

M E = 1,69   k N ⋅ m ↶

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se o cilindro E tem massa de 20 kg e cada segmento do cabo pode sustentar uma tração máxima de 400 N, determine a maior massa do cilindro F que pode ser suportada. Além disso, qual é a flecha y C ?
Se os cilindros E e F têm massa de 20 kg e 40 kg, respectivamente, determine a tração desenvolvida em cada cabo e a flecha y C .
Determine as forças normal e cortante e o momento fletor em uma seção passando pelo ponto C . Considere P=8k N .
Duas vigas estão presas ao membro vertical de modo que as conexões estruturais transmitem as cargas mostradas. Determine as forças normal e cortante e o momento fletor que atuam em uma seção que passa
Determine a distância a como uma fração do comprimento L da viga para localizar o suporte derolete de modo que o momento fletor na viga em B seja zero.