Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 101
Se os cilindros e têm massa de 20 kg e 40 kg, respectivamente, determine a tração desenvolvida em cada cabo e a flecha .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Temos aqui nesta questão um cabo submetido a duas cargas concentradas devido aos cilindros em em e .
Conhecendo estes pesos e parte da geometria do problema, precisamos calcular as trações em cada corda e o valor da flecha em .
Bom, por causa dessas informações que devemos encontrar, a questão dará um pouco de trabalho, pois temos que utilizar o método dos nós para cada um dos pontos e .
Mas, para isto, vamos utilizar o fato de que as trações nas cordas estão na direção das mesmas!
Sendo assim, vamos para as contas.
Passo 2
Como o nosso objetivo é analisar o equilíbrio em torno de cada nó, vamos começar analisando o nó . Esboçando o seu diagrama de corpo livre, temos:
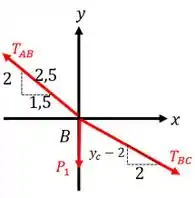
Aplicando as equações de equilíbrio, temos:
Reorganizando as duas equações, temos:
E aí vamos deixar elas paradas momentaneamente e vamos para o nó .
Passo 3
Agora vamos repetir o procedimento para o nó . Esboçando o seu diagrama de corpo livre, temos:
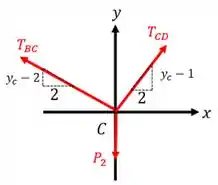
Aplicando as equações de equilíbrio, temos:
Reorganizando as duas equações, temos:
E assim conseguimos mais duas equações!
Passo 4
Agora vamos efetivamente calcular cada uma das nossas incógnitas, que totalizam 4 (trações em 3 cordas e a flecha ).
E, para que a gente determine estes parâmetros, vamos utilizar as quatro equações que obtivemos nos Passos 2 e 3 (Lembram das equações que guardamos momentaneamente???).
Juntando todas elas, teremos o seguinte sistema:
Agora é só resolvermos o sistema! Igualando a segunda com a quarta equação obtemos:
E ao substituirmos o valor da flecha nas outras equações obtemos:
E assim finalizamos a questão!