Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 7.Problemas - Ex. 17
Determine as forças normal e cortante e o momento fletor nos pontos e do elemento vertical.
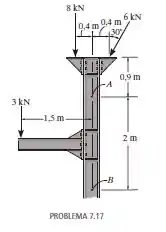
Passo 1
Opaaa.. beleza??
Nessa questão vamos usar as equações de equilíbrio:
- Somatório das forças em :
- em :
- e para o momento:
E já vamos começar cortando a barra onde interessa (até porque a barra neeem ta inteira no desenho).
Passo 2
Cortando no ponto :
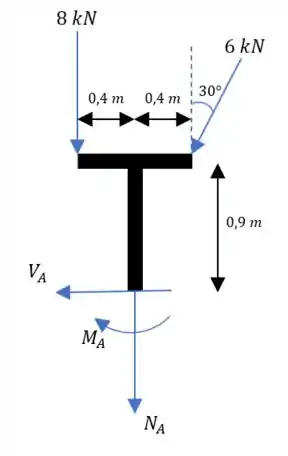
Fazendo o somatório das forças em :
Em :
E para o momento:
Passo 3
Agora fazendo o corte em :
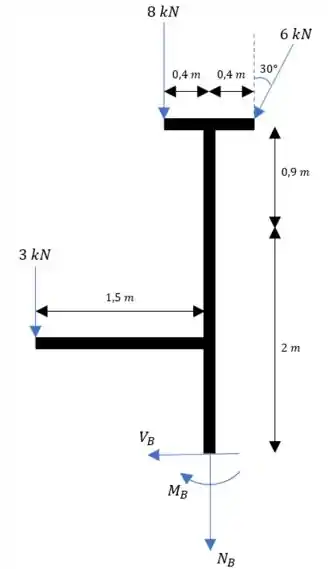
Fazendo o somatório das forças em :
Em :
E para o momento:
Ahhh... Repara que na resposta lá do final do livro as forças normal e cortante estão com sinais diferentes (estão positivas), mas isso não é erro. Apenas escolhemos a orientação diferentes das setinhas das forças, ok?
Essa acabamos. Bora mais uma?
Resposta
Exercícios de Livros Relacionados
Determine a força normal interna, o esforço cortante e o momento que atuam no ponto C . A unidade de resfriamento tem uma massa total de 225k g com centro de massa em G .
Determine a força normal interna, o esforço cortante e o momento no ponto D que está localizado à direita da força de 50N .
Determine a força normal interna, o esforço cortante e o momento nos pontos F e E da estrutura. A caixa pesa 1,5k N .
Determine a força normal interna, o esforço cortante e o momento atuando nos pontos B e C da barra curva.
143- A viga sustenta uma carga unitária uniforme w . Determine a posição x dos dois apoios de modo a minimizar o momento fletor máximo M m a x na viga. Especifique o valor de M m a x .